


Next: Problem 4 - Sorting
Up: Information Science I
Previous: Problem 2 - Cache
Answer the following questions on 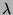 -calculus.
-calculus.
- 1.
- Give a
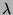 -term (
-term (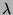 -expression) which has its normal
form, but may not reach its normal form depending on the order of reduction.
-expression) which has its normal
form, but may not reach its normal form depending on the order of reduction.
- 2.
- Give the definition of the Church-Rosser property.
- 3.
- Using the Church-Rosser property, prove that every
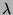 -term
has at most one normal form, where mutually
-term
has at most one normal form, where mutually 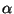 -convertible
-convertible
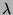 -terms are regarded as the same.
-terms are regarded as the same.
- 1.
- Let us consider the
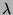 -expression
-expression
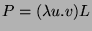 where
where
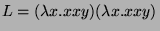 . If we
subsitute
. If we
subsitute 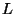 for
for 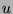 in
in 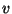 first then:
where
first then:
where 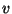 is a variable (that contains no
is a variable (that contains no 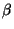 -redexes) and therefore a normal form: the normal form of
-redexes) and therefore a normal form: the normal form of 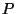 .
But, if we choose a different order for the reduction, then
.
But, if we choose a different order for the reduction, then 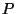 may not reach its normal form, such as in:
where we have first substituted
may not reach its normal form, such as in:
where we have first substituted
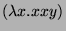 for
for 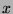 in
in
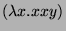 .
.
- 2.
- Here is the Church-Rosser theorem for
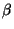 -reduction. It says that if
-reduction. It says that if
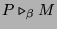 and
and
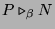 , then there exists
, then there exists 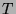 such that
such that
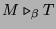 and
and
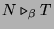 .
.
- 3.
- Let us suppose that the
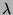 -expression
-expression 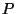 has two
has two 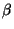 -normal forms
-normal forms 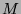 and
and 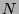 . We can also
write this:
As
. We can also
write this:
As 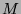 and
and 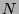 are
are 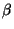 -normal forms, they do not contain any redexes. According to the Church-Rosser
theorem for
-normal forms, they do not contain any redexes. According to the Church-Rosser
theorem for 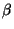 -reduction, there exists
-reduction, there exists 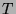 such that:
But, as
such that:
But, as 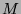 and
and 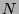 contain no redexes, it means that the
contain no redexes, it means that the 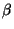 -reduction has just involved changes of
bound variables. In other words,
-reduction has just involved changes of
bound variables. In other words, 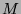 ,
, 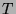 , and
, and 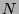 are
are 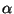 -congruent, i.e. mutually
-congruent, i.e. mutually 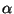 -convertible
-convertible
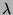 -terms inside these expression are regarded as being the same.
-terms inside these expression are regarded as being the same.



Next: Problem 4 - Sorting
Up: Information Science I
Previous: Problem 2 - Cache
Reynald AFFELDT
2000-06-08