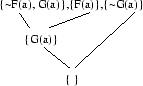![]() is a logical consequence of
is a logical consequence of
![]() means that for all the interpretations that
satisfy all the wffs of the set
means that for all the interpretations that
satisfy all the wffs of the set
![]() (these interpretations are also called
models of the set
(these interpretations are also called
models of the set
![]() ),
), ![]() is satified as well. The fact that
is satified as well. The fact that ![]() is
true in every model of
is
true in every model of
![]() is know as logical consequence. More precisely,
we say that
is know as logical consequence. More precisely,
we say that ![]() is then a logical consequence of
is then a logical consequence of
![]() or that
or that ![]() is logically
implied by
is logically
implied by
![]() . As a notation,
. As a notation,
![]() .
.
We want to prove that ![]() is a logical consequence of
is a logical consequence of ![]() and
and ![]() , i.e. that
, i.e. that
![]() is valid. We just need to refute
its negation
is valid. We just need to refute
its negation
![]() which the same as
which the same as
![]() . By refuting its negation, we
show that this negation is unsatisfiable, i.e. that no model assign it a true value, which
implies that its negation is always true (our definition of logical consequence).
. By refuting its negation, we
show that this negation is unsatisfiable, i.e. that no model assign it a true value, which
implies that its negation is always true (our definition of logical consequence).
We use ground resolution. We write the above CNF in the standard set notation using ground clauses
and check if the set of ground clauses is unsatisfiable. If we find the empty clause, then it means
that ![]() is a logical consequence of
is a logical consequence of ![]() and
and ![]() .
.