The block length of a Hamming code is given by
For 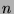 bits, we have
bits, we have 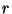 parity bits and
parity bits and 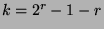 information bits.
Here
information bits.
Here 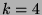 ,
,  , and
, and  . We begin with the parity-check matrix
. We begin with the parity-check matrix 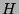 for
the systematic Hamming code. This matrix has
for
the systematic Hamming code. This matrix has 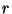 rows and
rows and 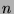 columns. The
first
columns. The
first 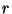 columns are specified as the
columns are specified as the 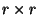 identity matrix. The
remaining
identity matrix. The
remaining 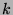 columns consist of nonzero binary vectors of length
columns consist of nonzero binary vectors of length 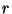 .
The form for the parity-check matrix for a systematic code is
The generator matrix
.
The form for the parity-check matrix for a systematic code is
The generator matrix 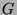 for the systematic code is
For all Hamming codes,
for the systematic code is
For all Hamming codes,
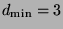 . We can use that code to correct a
single error. The codes may be decoded using a syndrome table. For the error
vector with its error in the
. We can use that code to correct a
single error. The codes may be decoded using a syndrome table. For the error
vector with its error in the 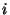 th column of
th column of 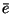 , the corresponding
syndrome is the
, the corresponding
syndrome is the 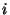 th row of
th row of  If we count bit positions in the error vector from left to right, starting
with 1, this position corresponds to the number obtained from reading the
symdrome from right to left, with the exception of syndromes 001 and 110.
If we count bit positions in the error vector from left to right, starting
with 1, this position corresponds to the number obtained from reading the
symdrome from right to left, with the exception of syndromes 001 and 110.
The code vector formed by 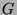 are of the form
And the parity generator has the following implementation:
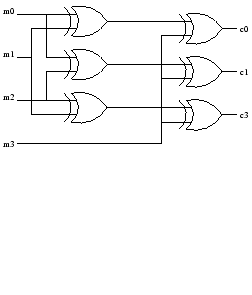
We recalculate the parity bits and compare them to the parity bits received:
are of the form
And the parity generator has the following implementation:
We recalculate the parity bits and compare them to the parity bits received:
There is a one-to-one mapping between the altered bit and the binary value
of
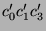 :
:
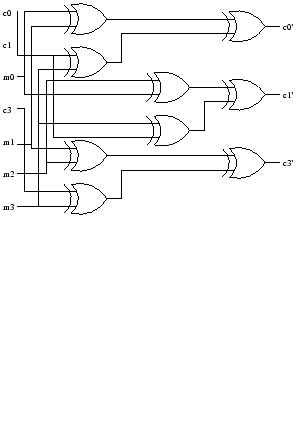
So that the following implementation points out the erronerous bits:
![$\displaystyle H=\left[\begin{array}{ccccccc}
1 & 0 & 0 & 1 & 1 & 0 & 1 \\
0 & 1 & 0 & 1 & 0 & 1 & 1 \\
0 & 0 & 1 & 0 & 1 & 1 & 1 \\
\end{array}\right]
$](img1148.png)
![$\displaystyle G = \left[\begin{array}{ccccccc}
1 & 1 & 0 & 1 & 0 & 0 & 0 \\
1...
...& 1 & 1 & 0 & 0 & 1 & 0 \\
1 & 1 & 1 & 0 & 0 & 0 & 1 \\
\end{array}\right]
$](img1151.png)

![$\displaystyle G = \left[\begin{array}{ccccccc}
1 & 1 & 1 & 0 & 0 & 0 & 0 \\
1...
...& 1 & 0 & 1 & 0 & 1 & 0 \\
1 & 1 & 0 & 1 & 0 & 0 & 1 \\
\end{array}\right]
$](img1156.png)
![$\displaystyle H=\left[\begin{array}{ccccccc}
1 & 0 & 1 & 0 & 1 & 0 & 1 \\
0 & 1 & 1 & 0 & 0 & 1 & 1 \\
0 & 0 & 0 & 1 & 1 & 1 & 1 \\
\end{array}\right]
$](img1157.png)
![]() :
:

![$\displaystyle H=\left[\begin{array}{ccccccc}
1 & 0 & 0 & 1 & 1 & 0 & 1 \\
0 & 1 & 0 & 1 & 0 & 1 & 1 \\
0 & 0 & 1 & 0 & 1 & 1 & 1 \\
\end{array}\right]
$](img1148.png)
![$\displaystyle G = \left[\begin{array}{ccccccc}
1 & 1 & 0 & 1 & 0 & 0 & 0 \\
1...
...& 1 & 1 & 0 & 0 & 1 & 0 \\
1 & 1 & 1 & 0 & 0 & 0 & 1 \\
\end{array}\right]
$](img1151.png)

![$\displaystyle G = \left[\begin{array}{ccccccc}
1 & 1 & 1 & 0 & 0 & 0 & 0 \\
1...
...& 1 & 0 & 1 & 0 & 1 & 0 \\
1 & 1 & 0 & 1 & 0 & 0 & 1 \\
\end{array}\right]
$](img1156.png)
![$\displaystyle H=\left[\begin{array}{ccccccc}
1 & 0 & 1 & 0 & 1 & 0 & 1 \\
0 & 1 & 1 & 0 & 0 & 1 & 1 \\
0 & 0 & 0 & 1 & 1 & 1 & 1 \\
\end{array}\right]
$](img1157.png)

![]() :
:

