Consider a typed ![]() -calculus, whose types and terms are given by the following syntax.
(We assume that constants and variables in
-calculus, whose types and terms are given by the following syntax.
(We assume that constants and variables in ![]() -prefixes are explicitly annotated with their types.)
-prefixes are explicitly annotated with their types.)
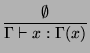
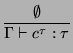
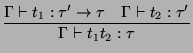
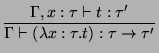
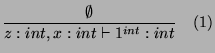
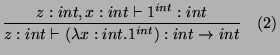
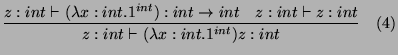
If
![]() ,
, ![]() reduces to
reduces to ![]() , then there is not type
mismatch, because this is a reduction with an empty serie of contractions or
changes of bound variables. According to (5), if
, then there is not type
mismatch, because this is a reduction with an empty serie of contractions or
changes of bound variables. According to (5), if ![]() reduces to
reduces to ![]() and
if
and
if
![]() , then
, then
![]() , which also means that
a non-empty serie of contractions or changes of bound variables doesn't cause
any type mismatch at run time.
, which also means that
a non-empty serie of contractions or changes of bound variables doesn't cause
any type mismatch at run time.