Problem 2 - BCH Codes

For a polynomial $x^4 + x + 1$ over $GF(2)$, let $\alpha$ be a root satisfying $\alpha^4 + \alpha + 1 = 0$.

1.

Show that $\alpha$, $\alpha^2$, ..., $\alpha^{15}$ are all mutually distinct.

2.

For a polynomial $f(x) = x^8 + x^7 + x^6 + x^4 + 1$ over $GF(2)$, show that $f(\alpha^4) = f(\alpha^3) = f(\alpha^2) = f(\alpha) = 0$ holds.

3.

Show that any nonzero polynomial in $\{ g(x)f(x) \; \vert \; g(x) \in GF(2)[x] \}$ as at least 5 nonzero coefficients.

1.

we calculate the following expressions:

$\alpha$
$\alpha^2$
$\alpha^3$
$\alpha^4$	=	$\alpha + 1$
$\alpha^5$	=	$\alpha^2 + \alpha$
$\alpha^6$	=	$\alpha^3 + \alpha^2$
$\alpha^7$	=	$\alpha^4 + \alpha^3$
	=	$\alpha + 1 + \alpha^3$
$\alpha^8$	=	$\alpha^2 + \alpha + \alpha^4$
	=	$\alpha^2 + 1$
$\alpha^9$	=	$\alpha^3 + \alpha$
$\alpha^{10}$	=	$\alpha^4 + \alpha^2$
	=	$\alpha^2 + \alpha + 1$
$\alpha^{11}$	=	$\alpha^3 + \alpha^2 + \alpha$
$\alpha^{12}$	=	$\alpha^4 + \alpha^3 + \alpha^2$
	=	$\alpha^3 + \alpha^2 + \alpha + 1$
$\alpha^{13}$	=	$\alpha^4 + \alpha^3 + \alpha^2 + \alpha$
	=	$\alpha^3 + \alpha^2 + 1$
$\alpha^{14}$	=	$\alpha^4 + \alpha^3 + \alpha$
	=	$\alpha^3 + 1$
$\alpha^{15}$	=	$\alpha^4 + \alpha$
	=	$1$
$\alpha^{16}$	=	$\alpha$

2.

$f(\alpha^4) = \alpha^{32} + \alpha^{28} + \alpha^{24} + \alpha^{16} + 1$
$= \alpha^{16}\alpha^{16} + \alpha^{16}\alpha^{12} + \alpha^{16}\alpha^{8} + \alpha + 1$
$= \alpha^2 + \alpha(\alpha^3+\alpha^2+\alpha+1)+\alpha(\alpha^2+1)+\alpha+1$
$= \alpha^2 + \alpha^4 + \alpha ^3 + \alpha^2 + \alpha + \alpha^3 + \alpha + \alpha + 1$
$= 0$

$f(\alpha^3) = \alpha^{24} + \alpha^{21} + \alpha^{18} + \alpha^{12} + 1$
$= \alpha^{16}\alpha^8 + \alpha^{16}\alpha^5 + \alpha^{16}\alpha^2 + \alpha^3 + \alpha^2 + \alpha + 1 + 1$
$= \alpha(\alpha^2+1) + \alpha(\alpha^2+\alpha) + \alpha^3 + \alpha^3 + \alpha^2 + \alpha$
$= \alpha^3 + \alpha + \alpha^3 + \alpha^2 + \alpha^2 + \alpha$
$= 0$

$f(\alpha^2) = \alpha^{16} + \alpha^{14} + \alpha^{12} + \alpha^8 + 1$
$= \alpha +\alpha^3 + 1 + \alpha^3 + \alpha^2 + \alpha + 1 + \alpha^2 + \alpha +1+1$
$= 0$

$f(\alpha) = \alpha^8 + \alpha^7 + \alpha^6 + \alpha^4 + 1$
$= \alpha^2 + 1 + \alpha + 1 + \alpha^3 + \alpha^3 + \alpha^2 + \alpha + 1 + 1$
$= 0$

3.

Let us assume that $c(x)\in\{ g(x)f(x) \; \vert \; g(x) \in GF(2)[x] \}$. We can denote $c(x)$ as being the following polynomial:

$$c(x)=c_0 + c_1x + c_2x^2 + \cdots + c_{n-1}x^{n-1}$$

$c(x)$ has the same zeros as $f(x)$, which leads to:

$$c(\alpha^i) = c_0 + c_1\alpha^i + c_2(\alpha^i)^2 + \cdots + c_{n-1}(\alpha_i)^{n-1} = 0, \quad i\in\{1,2,3,4\}$$

These equation can also be written as:

$$(c_0,c_1,c_2,\dots,c_{n-1})\left(\begin{array}{c} 1 \\ \alpha^i ... ...i)^2 \\ \vdots \\ (\alpha^i)^{n-1}\end{array}\right)=0, \quad i\in\{1,2,3,4\}$$

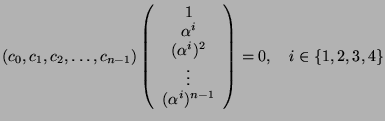
Let us now suppose that there exists a polynomial such that only four of its coefficients are non-zero. Then, we should have the following four relations:

$$(c_k,c_l,c_m,c_n)\left(\begin{array}{l} (\alpha^i)^k \\ (\alpha^i)^l \\ (\alpha^i)^m \\ (\alpha^i)^n \end{array}\right)=0, \quad i\in\{1,2,3,4\}$$

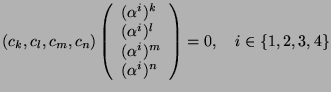
It implies in particular the following equality:

$$(c_k,c_l,c_m,c_n)\left(\begin{array}{llll} (\alpha^1)^k & (\alpha... ... (\alpha^1)^n & (\alpha^2)^n & (\alpha^3)^n & (\alpha^4)^n \end{array}\right)=0$$

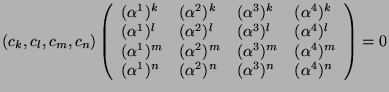
That means that the kernel of the linear application represented by the matrix is not $\{0\}$. This implies that the matrix is singular and therefore is determinant is zero. Let us take a closer look at it.

$$\left\vert\begin{array}{llll} (\alpha^1)^k & (\alpha^2)^k & (\alp... ...lpha^m)^3 \\ 1 & \alpha^n & (\alpha^n)^2 & (\alpha^n)^3 \end{array}\right\vert$$

$$= \alpha^{(k+l+m+n)}\Pi_{j<i, i,j\in\{k,l,m,n\}}(\alpha^i - \alpha^j)$$

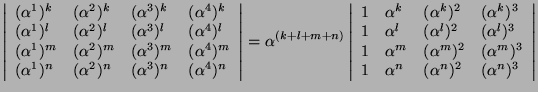
Which cannot be 0, obviously. Thus, our assumption that there exists a such polynomial was wrong. That's why a polynomial in $\{ g(x)f(x) \; \vert \; g(x) \in GF(2)[x] \}$ has at least five non-zero coefficients.