


Next: Information Science II
Up: Information Science I
Previous: Problem 7 - Operating
Put appropriate words/number in
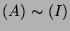 .
.
- 1.
- Concerning the Newton method for a nonlinear equation
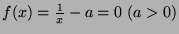 , when the initial value is set in the
interval
, when the initial value is set in the
interval 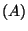 , it converges to
, it converges to
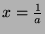 with the order of
convergence
with the order of
convergence 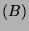 .
.
- 2.
- Apply the trapezoidal formula to the integral
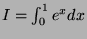 by dividing the interval into
by dividing the interval into 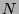 equal bins. The truncation error is
proportional to
equal bins. The truncation error is
proportional to  to the power
to the power 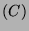 .
.
- 3.
- When solving an ordinary differential equation
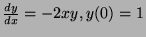 by the forward Euler method with interval
by the forward Euler method with interval 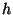 , the truncation error
at
, the truncation error
at  is proportional to
is proportional to 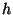 to the power
to the power 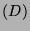 .
.
- 4.
- (Choose appropriate words by greek letters from the candidates shown
below. If multiple candidates are applicable, select the rightmost one.)
- The inverse of a nonsingular upper triangular matrix is (E).
- The inverse of a nonsingular band matrix is (F).
- The product of an upper triangular matrix and a lower triangular
matrix is (G).
- The product of a lower triangular matrix and an upper triangular
matrix is (H).
- A matrix which is upper and lower triangular is (I).
Candidates:
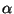 ) dense matrix,
) dense matrix, 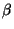 ) upper triangular matrix,
) upper triangular matrix, 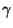 ) lower
triangular matrix,
) lower
triangular matrix, 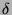 ) band matrix,
) band matrix, 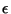 ) diagonal matrix.
) diagonal matrix.
- 1.
-
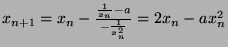
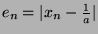
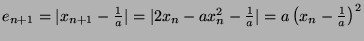
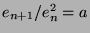
Thus  .
.
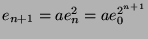
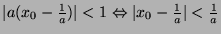
Thus
![$ (A) = [0,\frac{2}{a}]$](img189.png) .
.
- 2.
-
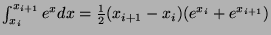
If
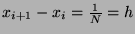 , the step lenght, then, the composite trapezium rule gives:
, the step lenght, then, the composite trapezium rule gives:
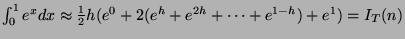
According to Hildebrand, with
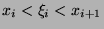 :
:
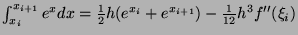
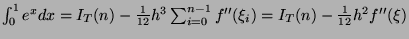
With 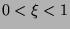 and
and
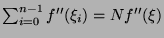 .
.
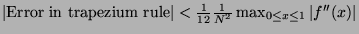
Thus 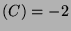 .
.
- 3.
-
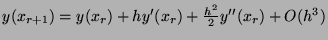
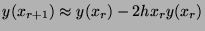
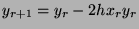
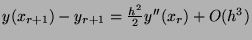
In particular:
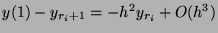
Thus 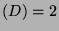 .
.
- 4.



Next: Information Science II
Up: Information Science I
Previous: Problem 7 - Operating
Reynald AFFELDT
2000-06-08
![]() .
.