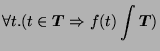Next: Problem 11 - Languages
Up: Information Science II
Previous: Problem 5 - Compilation
Let
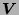 be a countably infinite set of variables, let
be a countably infinite set of variables, let 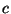 ba a constant symbol, and let
ba a constant symbol, and let 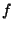 and
and
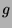 be function symbols. We define the set
be function symbols. We define the set
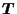 of terms as the least set closed under the
following rules:
of terms as the least set closed under the
following rules:
If variables
 are distinct from each other,
are distinct from each other,
![$ [t_1/x_1, \dots, t_n/x_n]t$](img1529.png) denotes the term
obtained from
denotes the term
obtained from 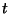 by replacing all the occurrences of each
by replacing all the occurrences of each
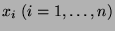 with
with 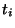 . We call
. We call
![$ \theta=[t_1/x_1, \dots, t_n/x_n]$](img1532.png) a substitution. Answer the following questions.
a substitution. Answer the following questions.
- 1.
- A substitution
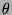 is called a unifier of
is called a unifier of 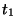 and
and 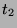 if it satisfies
if it satisfies
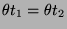 .
Check whether a unifier exists for the following each pair of terms. If so, answer a unifier.
.
Check whether a unifier exists for the following each pair of terms. If so, answer a unifier.
- 2.
- A unifier
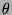 of
of 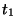 and
and 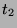 is called a most general unifier of
is called a most general unifier of 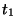 and
and 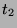 if, for any
unifier
if, for any
unifier 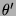 of
of 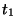 and
and 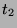 , there exists a substitution
, there exists a substitution 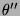 such that
such that
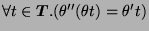 . Show that if both
. Show that if both 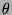 and
and 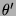 are
most general unifiers of
are
most general unifiers of 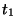 and
and 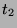 , then there is a substitution
, then there is a substitution
![$ [y_1/x_1, \dots, y_n/x_n]$](img1540.png) such that
such that
=\theta' t)$](img1541.png) and
and
 are mutually distinct variables.
(In other words, show the uniqueness of the most general unifier up to renaming of variables.)
are mutually distinct variables.
(In other words, show the uniqueness of the most general unifier up to renaming of variables.)
- 3.
- Prove that if there is a unifier of
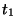 and
and 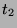 , then there is also a most general unifier of
, then there is also a most general unifier of
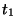 and
and 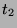 .
.
- 1.
-
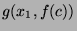 and
and
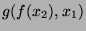 :
:
If
![$ \theta = [f(c)/x_1, c/x_2]$](img1543.png) , then
, then
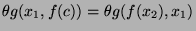 and
and 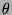 is a unifier.
is a unifier.
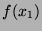 and
and 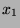 :
Since
:
Since
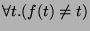 , there is no unifier for that pair of terms.
, there is no unifier for that pair of terms.



Next: Problem 11 - Languages
Up: Information Science II
Previous: Problem 5 - Compilation
Reynald AFFELDT
2000-06-08
![]() be a countably infinite set of variables, let
be a countably infinite set of variables, let ![]() ba a constant symbol, and let
ba a constant symbol, and let ![]() and
and
![]() be function symbols. We define the set
be function symbols. We define the set
![]() of terms as the least set closed under the
following rules:
of terms as the least set closed under the
following rules: