


Next: Problem 4 - Paging
Up: Information Science I
Previous: Problem 2 - Hardware
Consider the following formula:
- 1.
- Show that every interpretation with a finite domain satisfies the formula.
- 2.
- Find an interpretation which does not satisfy the formula.
- 1.
- Let us assume that we have an interpretation
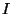 such that
such that 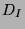 is finite. We want to show that the
above formula is always true under the valuation associated with
is finite. We want to show that the
above formula is always true under the valuation associated with 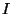 . To show that the implication
is true, we just have to show that the truth of
. To show that the implication
is true, we just have to show that the truth of
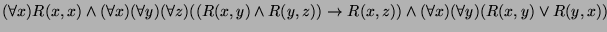 implies the
truth of
implies the
truth of
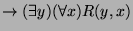 . So, we assume that the left-hand side of the
implication is true. It signifies in particular that:
is true. Let us choose
. So, we assume that the left-hand side of the
implication is true. It signifies in particular that:
is true. Let us choose  so that:
If for the whole set of variable ranging over
so that:
If for the whole set of variable ranging over 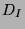 (which is finite),
(which is finite), 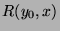 is true, then it is
over. If not, we consider one of the
is true, then it is
over. If not, we consider one of the 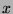 such that
such that 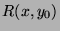 . We call it
. We call it 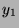 and for that
and for that 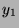 we have:
But now, we do know that the set of
we have:
But now, we do know that the set of 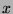 verifying
verifying 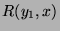 contains at least one element (
contains at least one element ( ). In the
same way we build
). In the
same way we build 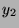 .
Let us assume that the cardinality of
.
Let us assume that the cardinality of 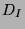 is
is 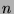 and that we have just built
and that we have just built 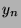 , that is:
Where the set of
, that is:
Where the set of 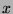 verifying
verifying 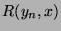 contains
contains
 . I have succeeded in
finding a
. I have succeeded in
finding a 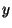 such that:
We conclude by saying that all interpreation
such that:
We conclude by saying that all interpreation 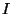 where
where 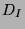 is finite satisfies the wff.
is finite satisfies the wff.
- 2.
- If you choose the interpreation
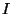 with
with
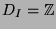 and
and 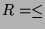 then the wff states that:
which is obviously false.
then the wff states that:
which is obviously false.



Next: Problem 4 - Paging
Up: Information Science I
Previous: Problem 2 - Hardware
Reynald AFFELDT
2000-06-08