Problem 10 - Coding

In a single-variable polynomial ring $GF(2)[x]$ whose coefficients are elements of the finite field $GF(2)$ of size 2, an irreductible polynomial $g(x)$ of degree $l$ is said to be primitive it it divides $x^n-1$ for $n=2^l-1$ and it does not divide $x^m-1$ for any $m$ with $0\leq m < n$.

1.

Show that $1+x+x^3$ with $l=3$ is a primitive polynomial.

2.

Consider residue-class ring $R=GF(2)[x]/(x^n-1)$ of $GF(2)[x]$ by an ideal $(x^n-1)$ generated by $x^n-1$. With a polynomial $f(x)=c_0+c_1x+\cdots+c_{n-1}x^{n-1}$ in $R$, associate a vector $(c_0, c_1, \dots, c_{n-1})$. Let $S$ be a set of all vectors associated with polynomials in an ideal generated by a primitive polynomial $g(x)$ of degree $l$ in $R$. Then, show that the Hamming distance between any pair of distinct vectors is at least 3.

1.

We first show that $1+x+x^3$ does divide $x^7-1$ but does not divide $x^6-1, x^5-1, x^4-1,$ and $x^3-1$.

$$\begin{array}{l\vert l} x^7 - 1 & x^3 + x + 1 \\ \hline -x... ...+1 & \\ -x^4-x^2-x & \\ x^3+x+1 & \\ 0 & \\ \end{array}$$

$$\begin{array}{l\vert l} x^6 - 1 & x^3+x+1 \\ \hline -x^6-x... ... \\ x^3+x^2+x+1 & \\ -x^3-x-1 & \\ x^2 & \\ \end{array}$$

$$\begin{array}{l\vert l} x^5-1 & x^3+x+1 \\ \hline -x^5-x^3... ... \\ x^3+x^2+1 & \\ -x^3-x-1 & \\ x^2+x & \\ \end{array}$$

$$\begin{array}{l\vert l} x^4-1 & x^3+x+1 \\ \hline -x^4-x^2-x & x \\ x^2+x+1 & \\ \end{array}$$

$$\begin{array}{l\vert l} x^3-1 & x^3 + x + 1 \\ \hline -x^3-x-1 & 1 \\ x & \\ \end{array}$$

Of course, $1+x+x^3$ does not divide $x^2-1, x-1,$ nor 0.

2.

$R=GF(2)[x]/(x^n-1)$ is the set of polynomials modulo $x^n-1$. It forms a mathematical structure called a ring. As far as the question is concerned, we take a closer look at $S=GF(2)[x]/\hbox{I}$ where $I$ is an ideal generated by a primitive polynomial $g(x)$ of degree $l$. Of course, we take the previous polynomial (which is primitive) as our primitive polynomial $g(x)$. Therefore:

$$g(x) = 1+x+x^3.$$

With every polynomial $f(x)=c_0 + c_1x + c_2x^2 + c_3x^3 + c_4x^4 + c_5x^5 + c_6x^6$, we associate a vector $(c_0,c_1,c_2,c_3,c_4,c_5,c_6)$. We therefore need I to be an ideal such that every polynomial of $S$ has a degree which is at most 6. We can choose the ideal given by:

$$x^7 - 1 = (1 + x + x^3)(1 + x + x^2 + x^4).$$

Thus, in factm we have $S=GF(2)[x]/(x^7-1)$.

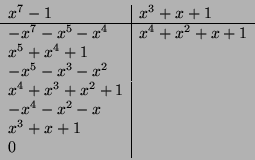
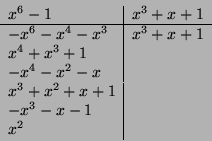
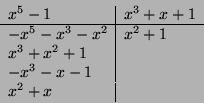
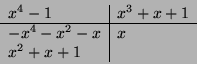
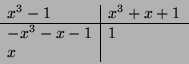
We are asked to show that the minimum Hamming code is 3. What is the link with the the above ring? We know that we can represent cyclic codes thank to polynomials. $S$ will in fact be the set of our code words. It precisely contains $2^7$ distinct polynomials. Because we want to achieve a code word length of 7, we need a generator polynomial $g(x)$ and a message polynomial $m(x)$ of the right length. Our cyclic code generator polynomial is constructed from the factors of $x^7-1$. As $\deg[g(x)]=3$, $\deg[m(x)]\leq 3$:

$$c(x)=(m_0+m_1x+m_2x^2+m_3x^3)(1+x+x^3).$$

We below list all the possible messages and for each one the corresponding code word.

$$\begin{array}{llll} \hline m(x) & c(x) & m(x) & c(x) \\ \h... ...& 1+x+x^2+x^3 & 1+x+x^2+x^3+x^4+x^5+x^6 \\ \hline \end{array}$$

There, we notice that the minimum Hamming weight of the nonzero code words is 3, and therefore, this code has a minimum Hamming distance of 3.