


Next: Problem 4 - Compilation
Up: Information Science I
Previous: Problem 2 - Operating
Let us define a set
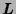 of terms inductively as follows (
of terms inductively as follows (
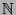 is the set of natural
numbers):
is the set of natural
numbers):
Answer the following questions.
- 1.
- Prove that there is exactly one total function
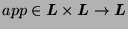 that satisfies the following equations:
that satisfies the following equations:
- 2.
- Prove that the above function
 satisfies
satisfies
- 1.
- Let us suppose that we have two applications
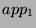 and
and 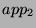 described as above. We want to show
that
described as above. We want to show
that
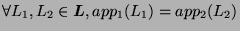
- If
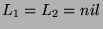 , then
, then
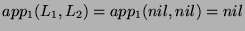 and
and
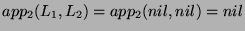 .
Thus
.
Thus
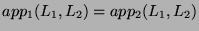 .
.
- If
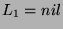 and
and
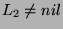 , then
, then
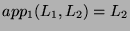 and
and
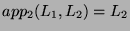 . Thus
. Thus
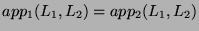 .
.
- If
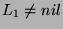 and
and 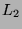 is either
is either 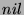 or not. We first suppose that
or not. We first suppose that
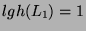 . Then
. Then
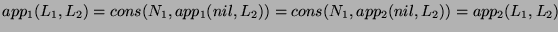 as seen above.
Let us suppose that this is true for
as seen above.
Let us suppose that this is true for
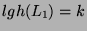 . Then, let's choose
. Then, let's choose 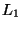 so that
so that
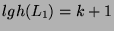 . Then
we have
. Then
we have
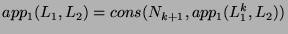 . By the inductive hypothesis, we have
. By the inductive hypothesis, we have
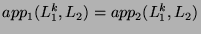 . Then, it means that
. Then, it means that
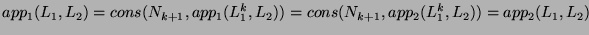 . Therefore the property is proven for all the kinds of couple
. Therefore the property is proven for all the kinds of couple
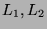 that can occur.
that can occur.
- 2.
- We shall prove the property inductively on the length of
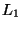 . Let us first suppose that
. Let us first suppose that 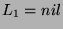 . Then,
we have:
. Then,
we have:
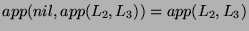 (according to the definition of
(according to the definition of  )
)
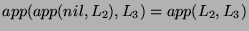 (since
(since
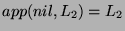 )
)
Thus, the property is true for
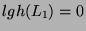 . Let us now suppose that the property is also true for
. Let us now suppose that the property is also true for
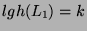 . Does it hold for
. Does it hold for
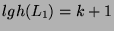 ?
?
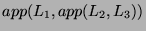
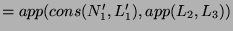 with
with
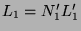
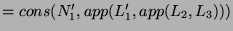 by the definition of
by the definition of 
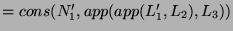 by the inductive hypothesis
by the inductive hypothesis
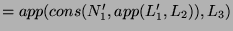 by the definition of
by the definition of 
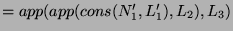 by the definition of
by the definition of 
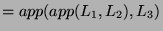 by the definition of
by the definition of 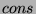
We have shown the proof by induction.



Next: Problem 4 - Compilation
Up: Information Science I
Previous: Problem 2 - Operating
Reynald AFFELDT
2000-06-08
![]() of terms inductively as follows (
of terms inductively as follows (
![]() is the set of natural
numbers):
is the set of natural
numbers):