Problem 1 - Automata

Show the deterministic finite automaton with the minimum number of states which accepts the same language as the following non-deterministic finite automaton. Also, find the regular expression for this language. Here, the alphabet is assumed to be ${a, b}$.

$$\includegraphics{nfa.ps}$$

$$\includegraphics{nfa2.ps}$$

• The original NFA is $M=(\Sigma, Q, \delta, q_0, F)$ where $\Sigma = \{a,b\}$, $Q=\{q_0,\dots,q_8\}$, $F=\{q_0\}$. The construct a DFA $M'=(\Sigma, Q', \delta', [q_0], F')$ where $Q'$ is the set of all the subsets of $Q$ and $[q_0]=q_0$ is the initial state of our DFA.

  $\delta'([q_0],a)=[q_1,q_6]$
  $\delta'([q_0],b)=\emptyset$

  $\delta'([q_1,q_6],a)=\emptyset$
  $\delta'([q_1,q_6],b)=[q_2,q_7]$

  $\delta'([q_2,q_7],a)=[q_3,q_8]$
  $\delta'([q_2,q_7],b)=\emptyset$

  $\delta'([q_3,q_8],a)=\emptyset$
  $\delta'([q_3,q_8],b)=[q_0,q_4]$

  $\delta'([q_0,q_4],a)=[q_5,q_1,q_6]$
  $\delta'([q_0,q_4],b)=\emptyset$

  $\delta'([q_5,q_1,q_6],a)=\emptyset$
  $\delta'([q_5,q_1,q_6],b)=[q_0,q_2,q_7]$
  

  $\delta'([q_0,q_2,q_7],a)=[q_1,q_6,q_3,q_8]$
  $\delta'([q_0,q_2,q_7],b)=\emptyset$

  $\delta'([q_1,q_6,q_3,q_8],a)=\emptyset$
  $\delta'([q_1,q_6,q_3,q_8],b)=[q_2,q_7,q_4,q_0]$

  $\delta'([q_2,q_7,q_4,q_0],a)=[q_3,q_8,q_5,q_1,q_6]$
  $\delta'([q_2,q_7,q_4,q_0],b)=\emptyset$

  $\delta'([q_3,q_8,q_5,q_1,q_6],a)=\emptyset$
  $\delta'([q_3,q_8,q_5,q_1,q_6],b)=[q_4,q_0,q_2,q_7]$

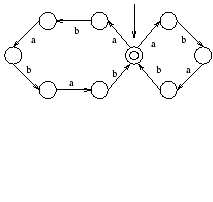
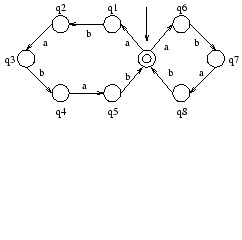
  We therefore have the following states:
  $Q_0 = [q_0]$
  $Q_1 = [q_1,q_6]$
  $Q_2 = [q_2,q_7]$
  $Q_3 = [q_3,q_8]$
  $Q_4 = [q_0,q_4]$
  $Q_5 = [q_5,q_1,q_6]$
  $Q_6 = [q_0,q_2,q_7]$
  $Q_7 = [q_1,q_6,q_3,q_8]$
  $Q_8 = [q_2,q_7,q_4,q_0]$
  $Q_9 = [q_3,q_8,q_5,q_1,q_6]$

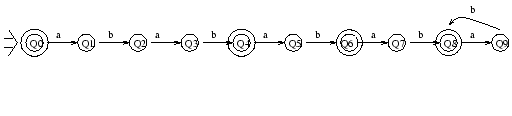
  Among the final states, we have:
  $Q_0, Q_4, Q_6, Q_8$

  $$\includegraphics{nfa-to-dfa.ps}$$

• We consider the following relation: $p\equiv q$ iff for each input string $x$, $\delta(p,x)$ is an accepting state iff $\delta(q,x)$ is an accepting state.

  We place a cross in the following figure when a final state and a non-final state are opposed (they can't be equivalent).

  $$\includegraphics{dfa-to-sdfa.ps}$$
  Then a lot of pairs cannot be equivalent because they only accpet different inputs (e.g., $(2,1)$).

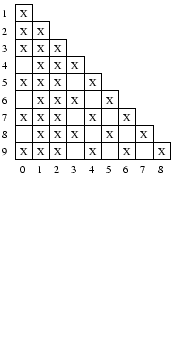
  We consider the other states. For instance, $(3,1)$. $\delta(3,b)=4$ and $\delta(1,b)=2$ and there is a cross at $(4,2)$, this means $(3,1)$ is not a pair of equivalent states.

  We repeat these operations, in that order, until we find a fixed point.

  We finally get the following states:
  $(0,8,6,4)$
  $(3,9,7,5)$
  $1$
  $2$

  $$\includegraphics{sdfa.ps}$$

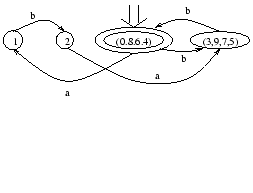
  The corresponding regular expression is:
  $\epsilon + abab(ab)^*$