Problem 8 - Algorithms

For $n$ finite intervals $I_i = [a_i,b_i] \; (i=1,\dots,n)$ on a line such that $2n$ numbers $a_i$, $b_i$ $(i=1,\dots,n)$ are distinct, answer the following questions.

1.

Give an efficient algorithm to find a maximum-size subset of mutually non-intersecting intervals, and estimate its time complexity.

2.

Give an efficient coloring algorithm to color each intervals with minimum number of colors so that any two intersecting intervals are colored by different ones, and estimate its time complexity.

1.

For each sequence of $n$ finite intervals we can construct the following graph. The set of vertices is made equalt to the set of intervals. Each vertex corresponds to an interval and both of them are given the same identity number ( $1\leq i\leq n$). There is an edge between $i$ and $j$ if and only if the quantity $a_j-b_i$ is positive, i.e., there is an edge between two vertices if and only if the intervals do not overlap. The edge is oriented from $i$ to $j$ if and only if $j>i$. In this graph, a path is a valid sequence of intervals, i.e., it contains mutually non-intersecting intervals. The figure below show an instance of the problem in (a). Notice that the graph has no cycle; by construction, it is only possible to go forward in the set of nodes.

$$\includegraphics{sequence-of-intervals.ps}$$

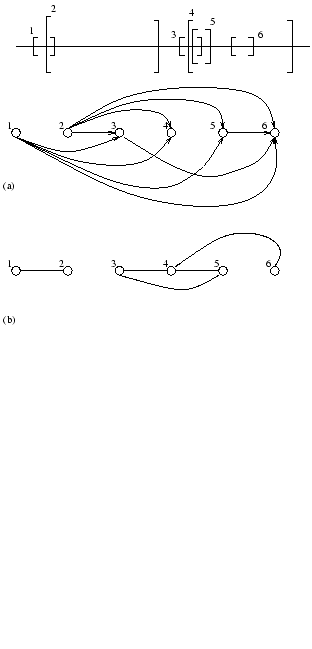
From each vertex, we just have to check all the possible (directed) paths and remember them. The longest will denote a maximum-size subset of mutually non-intersecting intervals. How do we actually look for it?

There is a val array of $n$ integers associated with the set of intervals. There is also a dad array of $n$ integers to remember the father of each node in a longest path. We select the first node and put is val value to 0. dad is initializes to 0 too. We check all the adjacent nodes and put their val values to 1, or, more precisely, to val of the predecessor plus 1. Their dad values are given the number associated with the predecessor node. Then we perform the same operations for any following nodes taken in the increasing order. Let us consider node $i$. If val$[i]$ has not been yet initialized, we initialize val$[i]$ and dad$[i]$ to 0. We look for the adjacent nodes $j$ and determine their val and dad values: if val$[i]+1$ is greater than val$[j]$, we update val and dad (the latter is given the value of $i$); if not, it means that $j$ is reachable through a longer path that we prefer to keep track of.

The node with the higher val value is the last node of a longest path. Reading the dad array in reverse order gives us the element of that path. We need to go through all nodes onces and for each of them we look at a subset of a partition of the edges, leading to a $O(V+E)$ algorithm. $\vert V\vert=n$ and $\vert E\vert$ cannot exceed $\vert V\vert^2$. Thus, we have a $O(n^2)$ algorithm.

2.

We can represent the problem of coloring as in the figure above (b). Each vertex represents an interval that is linked to another vertex if and only if they overlap. Our problem can be understood as the problem of coloring the graph constructed this way.