


Next: Problem 2 - Analysis
Up: Mathematics
Previous: Mathematics
Compute the maximal and minimal values of the following functions.
- 1.
-
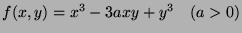
- 2.
-
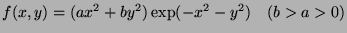
Taylor-Young formula with
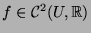 with
with
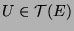 :
:
We call Monge notation the particular case where
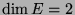 :
:
where
If
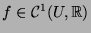 where
where
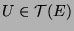 , we say that
, we say that 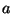 is a
critical point when
is a
critical point when 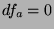 .
.
We assume that
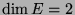 . Let
. Let
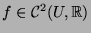 with
with
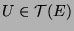 and let
and let
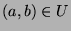 be a critical point of
be a critical point of 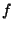 such that
such that
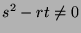 at
at 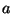 :
:
- If
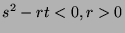 ,
, 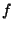 has a minimal value at
has a minimal value at 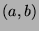 .
.
- If
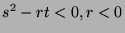 ,
, 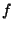 has a maximal value at
has a maximal value at 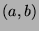 .
.
- If
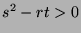 ,
, 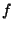 has neither a minimal value nor a maximal value at
has neither a minimal value nor a maximal value at 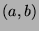 .
.
- 1.
-
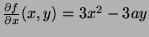
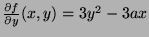
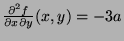
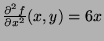
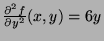
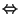
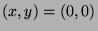
At
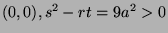
Therefore, 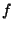 has no extremum.
has no extremum.
- 2.
-
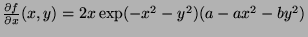
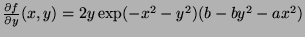
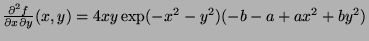
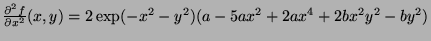
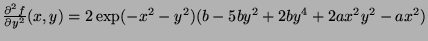
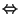
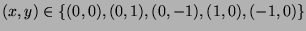
- At
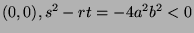 , we a minimum (because
, we a minimum (because
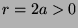 ) of value 0.
) of value 0.
- At
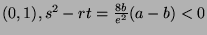 , we have a maximum (because
, we have a maximum (because 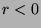 ) of value
) of value
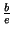 .
.
- At
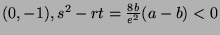 , we have a maximum (because
, we have a maximum (because 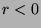 ) of value
) of value
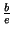 .
.
- At
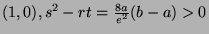 , we don't have any extremum.
, we don't have any extremum.
- At
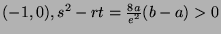 , we don't have any extremum.
, we don't have any extremum.



Next: Problem 2 - Analysis
Up: Mathematics
Previous: Mathematics
Reynald AFFELDT
2000-06-08
![]() with
with
![]() :
:
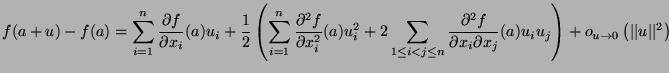
![]() :
:
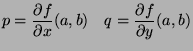
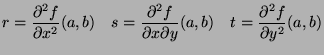
![]() where
where
![]() , we say that
, we say that ![]() is a
critical point when
is a
critical point when ![]() .
.
![]() . Let
. Let
![]() with
with
![]() and let
and let
![]() be a critical point of
be a critical point of ![]() such that
such that
![]() at
at ![]() :
: