Next: Problem 4 - Operating
Up: Information Science I
Previous: Problem 2 - Digital
Consider an information source consisting of 5 characters 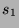 ,
, 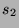 ,
,
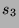 ,
, 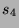 ,
, 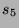 with probability
with probability
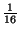 ,
,
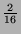 ,
,
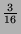 ,
,
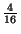 ,
,
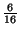 respectively.
respectively.
- 1.
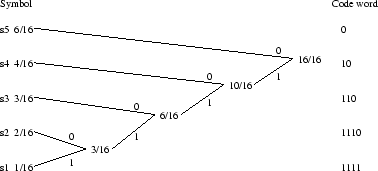
- Find a Huffman code for this information source, and compute the
average code length, where
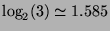 .
.
- 2.
- Compute the entropy of this information source
- 3.
- Describe relation between the entropy and the average code length.
- 1.
- The code words are:
The average code length is:
- 2.
- The entropy is:
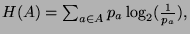
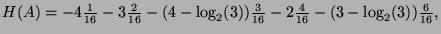
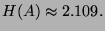
- 3.
- The efficiency of the code is:
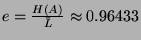
which means that only  of the bits are redundant.
of the bits are redundant.
We can also point out that:
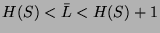
Huffman code can deliver code word sequence that asymptotically approach
the entropy. Which means that for large source alphabet, the amount of
redundant bits is very small.
Reynald AFFELDT
2000-06-08
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() with probability
with probability
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() respectively.
respectively.