


Next: Problem 2 - Digital
Up: Information Science I
Previous: Information Science I
- 1.
- Transform the following logic formula to a prenex normal form with Skolem variables:
where
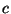 is a constant.
is a constant.
- 2.
- Find the minimal Herdrand model for the resultant logic formula. Here, consider only the
symbols appearing in the formula. Also, the minimal Herbrand model is a minimal subset among
subsets of Herbrand bases.
Herbrand universe:
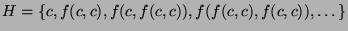
Ground terms:
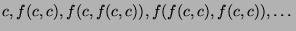
Ground atoms:
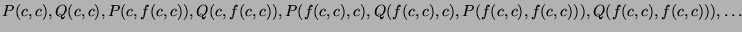
Herbrand base:
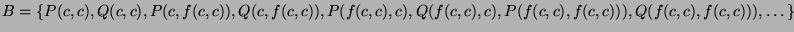
Herbrand interpretation:  ,
,
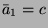 ,
,
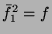 ,
there are no restrictions on the assignments of relations over the Herbrand universe to predicates.
,
there are no restrictions on the assignments of relations over the Herbrand universe to predicates.
Herbrand model: Just choose a subset of the Herbrand base and assign to its elements the  value.
value.
Then, the minimal Herbrand model here is:
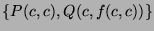 .
.
Reynald AFFELDT
2000-06-08
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
there are no restrictions on the assignments of relations over the Herbrand universe to predicates.
,
there are no restrictions on the assignments of relations over the Herbrand universe to predicates.
![]() value.
value.
![]() .
.