


Next: Problem 2 - Probability
Up: Mathematics
Previous: Mathematics
For an
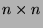 square matrices
square matrices 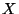 ,
, 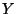 , define
, define ![$ [X,Y]$](img1199.png) by
by
Prove the following:
- 1.
- When
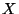 ,
, 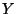 are alternating matrices,
are alternating matrices, ![$ [X,Y]$](img1199.png) is also an alternating matrix, where
is also an alternating matrix, where 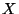 is an
alternating matrix if
is an
alternating matrix if
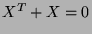 is satisfied.
is satisfied.
- 2.
-
- 1.
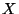 and
and 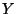 are alternating matrices, that is:
We want to check whether we have
are alternating matrices, that is:
We want to check whether we have
![$ [X,Y]=-[X,Y]^T$](img1204.png) or not.
or not.
![$ [X,Y]^T = (XY-YX)^T,$](img1205.png)
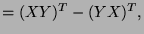
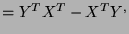

![$ =-[X,Y]$](img1209.png)
- 2.
- The terms we eliminate at each step are in bold.
![$ [X,[Y,Z]]+[Y,[Z,X]]+[Z,[X,Y]]$](img1210.png)
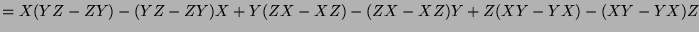
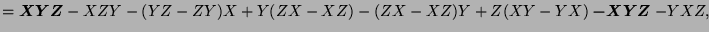
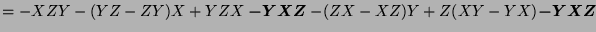
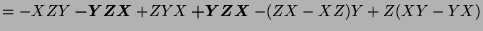
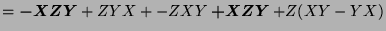
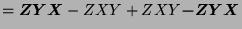
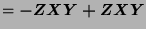
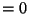
Reynald AFFELDT
2000-06-08
![]() square matrices
square matrices ![]() ,
, ![]() , define
, define ![]() by
by