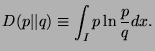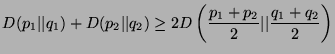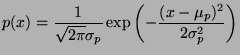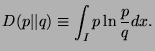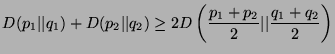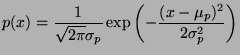Next: Information Science I
Up: Mathematics
Previous: Problem 1 - Matrices
- 1.
- Let
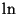 by the natural logarithm. Show that
by the natural logarithm. Show that
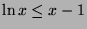 for
for 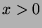 .
.
- 2.
- For probability density functions
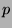 and
and 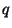 of random variable
of random variable
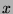 on a domains
on a domains 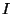 ,
, 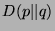 is defined by
Show that
is defined by
Show that
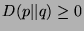 holds. When does this inequality hold by equality?
holds. When does this inequality hold by equality?
- 3.
- For probability density functions
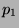 ,
, 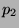 ,
, 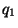 ,
, 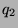 of
random variable
of
random variable 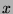 , show
, show
- 4.
- Let
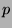 ,
,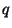 be normal distributions with mean
be normal distributions with mean 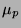 ,
, 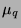 and
standard deviation
and
standard deviation 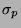 ,
, 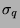 , respectively (i.e.
, respectively (i.e. 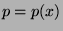 is
given by
and similar for
is
given by
and similar for 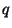 ). Compute
). Compute 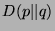 .
.
- 1.
- Let us consider the following function
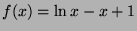 . Its first derivative is
. Its first derivative is
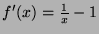 .
This function is positive if
.
This function is positive if 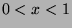 , negative is
, negative is 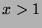 and is 0 if
and is 0 if  . Thus
. Thus 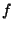 is increasing from
is increasing from 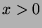 to
to 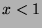 , it reaches 0 in 1 and then decreases for
, it reaches 0 in 1 and then decreases for 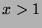 . Thus,
. Thus,
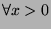 ,
,
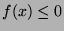 . That is:
. That is:
- 2.
-
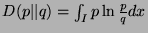
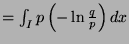
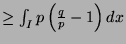
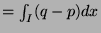
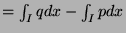
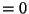 since both
since both
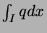 and
and
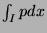 are equal to 1.
are equal to 1.
- 3.
-
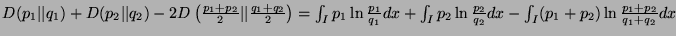
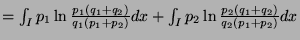
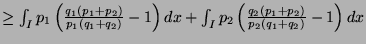
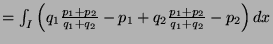
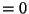
- 4.
-
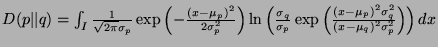
TODO: What am I supposed to find?



Next: Information Science I
Up: Mathematics
Previous: Problem 1 - Matrices
Reynald AFFELDT
2000-06-08