Problem 4 - Predicate Logic

1.

Transform the following logical formula into clausal forms:

$$\forall x \forall y P(x, y) \rightarrow Q(x, y)$$

$$\neg \forall x \exists y P(x, y) \rightarrow Q(x, y)$$

2.

Using linear resolution , show that the following set of clauses is unsatisfiable:

$$\{A, B\}, \{B, C\}, \{C, D\}, \{\neg C, \neg A\}, \{\neg D, \neg B\}, \{\neg B, \neg C\}$$

Prenex form: $\forall x \forall y P(x, y) \rightarrow Q(x, y)$.

Skolemized form: $\forall x \forall y P(x, y) \rightarrow Q(x, y)$.

Without universal quantifiers: $P(x, y) \rightarrow Q(x, y)$.

Adequate connectives: $\neg P(x, y) \vee Q(x, y)$.

Conjunctive normal form (or clausal form): $\neg P(x, y) \vee Q(x, y)$.

Prenex form: $\exists x \forall y \neg (P(x, y) \rightarrow Q(x, y))$.

Skolemized form: $\forall y \neg (P(c_1, y) \rightarrow Q(c_1, y))$.

Without universal quantifiers: $\neg (P(c_1, y) \rightarrow Q(c_1, y))$.

Adequate connectives: $\neg (\neg P(c_1, y) \vee Q(c_1, y)) = P(c_1, y) \wedge \neg Q(c_1, y)$.

Truth table:

$\neg$	$P(c_1, y)$	$\wedge$	$\neg$	$Q(c_1, y)$
T	T	F	F	T
F	T	T	T	F
T	F	F	F	T
T	F	F	T	F

Disjonctive normal form:

$\neg \left((P(c_1, y) \wedge Q(c_1, y)) \vee (\neg P(c_1, y) \wedge Q(c_1, y)) \vee (\neg P(c_1, y) \wedge \neg Q(c_1, y))\right)$.

De Morgan's law yiels a conjunctive normal form (or clausal form):

$(\neg P(c_1, y) \vee \neg Q(c_1, y)) \wedge (P(c_1, y) \vee \neg Q(c_1, y)) \wedge (P(c_1, y) \vee Q(c_1, y))$.

We use the following resolution rule:

$$C_1 \cup \{l\}, C_2 \cup \{l^c\} \vdash C_1 \cup C_2$$

where $C_i$ is a clause and $l^j$ a literal. The wffs are considered to be written in CNF using the standard set notation. $C_i$ is refered to as a parent clause and $C_1 \cup C_2$ is refered to as the resolvent.

In a linear resolution, we follow the standard resolution procedure but we take care of the fact that the previous resolvent is always a parent clause of the next resolution.

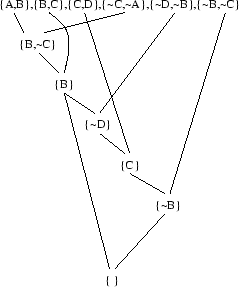
We yield the empty clause, that means that we set of clauses is not satisfiable, i.e., there is no interpretation thanks to which this set can be given a true value.