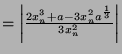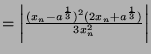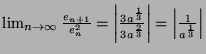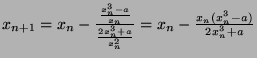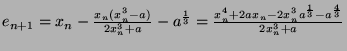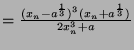Problem 5 - Newton-Raphson method

1.

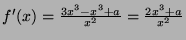
Explain the Newton-Raphson method solving a nonlinear equation 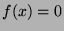$f(x)=0$ on a variable $x$.

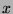2.

Derive two methods of computing the cube root of a given number using the Newton-Raphson method, and analyse their features.

1.

2.

$f(x)=x^3 - a$
$x_{n+1} = x_n - \frac{x_n^3 - a}{3 x_n^2}$
$e_{n} = \left\vert x_n - a^{\frac{1}{3}} \right\vert$
$e_{n+1} = \left\vert x_n - \frac{x_n^3 - a}{3x_n^2} - a^{\frac{1}{3}}\right\vert$
$=\left\vert \frac{2x_n^3 + a - 3x_n^2 a^{\frac{1}{3}}}{3x_n^2} \right\vert$
$=\left\vert \frac{(x_n-a^\frac{1}{3})^2(2x_n + a^{\frac{1}{3}})}{3x_n^2} \right\vert$
Thus $\lim_{n\rightarrow \infty} \frac{e_{n+1}}{e_n^2} = \left\vert \frac{3a^\frac{1... ...{3a^{\frac{2}{3}}} \right\vert = \left\vert \frac{1}{a^\frac{1}{3}} \right\vert$
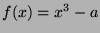
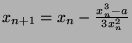
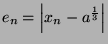
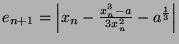
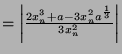
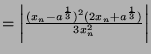
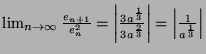
Thus the order of convergence is 2.

$f(x)=\frac{x^3 - a}{x}$
$f'(x)=\frac{3x^3 - x^3 + a}{x^2} = \frac{2x^3 + a}{x^2}$
$x_{n+1} = x_n - \frac{\frac{x_n^3-a}{x_n}}{\frac{2x_n^3+a}{x_n^2}} = x_n - \frac{x_n(x_n^3-a)}{2x_n^3+a}$
$e_n = x_n - a^\frac{1}{3}$
$e_{n+1} = x_n - \frac{x_n(x_n^3 - a)}{2x_n^3 + a} - a^\frac{1}{3} = \frac{x_n^4 + 2a x_n -2x_n^3 a^\frac{1}{3} - a^\frac{4}{3}}{2x_n^3 + a}$
$= \frac{(x_n-a^\frac{1}{3})^3(x_n+a^\frac{1}{3})}{2x_n^3 + a}$
Thus $\lim_{n\rightarrow \infty} \frac{e_{n+1}}{e_n^3} = \frac{2a^\frac{1}{3}}{3a}$
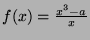
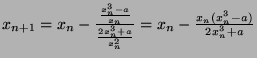
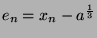
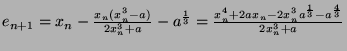
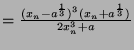
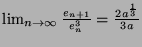
Thus the order of convergence is 3.