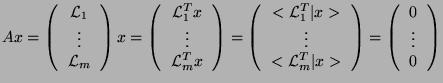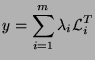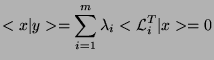Next: Information Science I
Up: Mathematics
Previous: Problem 1 - Differentiable
Let 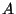 be an
be an
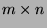 real matrix (
real matrix (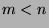 ) whose rank is
) whose rank is 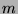 . Define
. Define 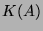 in the
in the 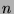 -dimensional real
vector space
-dimensional real
vector space
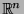 as follows:
as follows:
Answer the following questions:
- 1.
- Show that
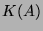 is a vector subspace. Give its rank.
is a vector subspace. Give its rank.
- 2.
- Let
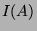 be the space spanned by the vectors obtained by transposing the rows of
be the space spanned by the vectors obtained by transposing the rows of 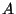 . Show that
the vectors in
. Show that
the vectors in 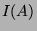 and the vectors in
and the vectors in 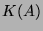 are orthogonal.
are orthogonal.
- 3.
- For a vector
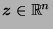 , derive the form of
, derive the form of
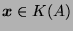 and
and
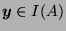 that achieve, repectively, the minimum in the following:
that achieve, repectively, the minimum in the following:
Here, 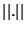 represents the
represents the 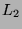 norm and
norm and
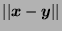 is the Euclidean distance
between
is the Euclidean distance
between
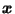 and
and
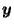 .
.
- 1.
- We know that
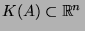 and that
and that
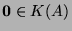 . Moreover,
Thus,
. Moreover,
Thus, 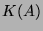 is a vector subspace of
is a vector subspace of
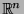 .
.
According to the rank theorem, we have
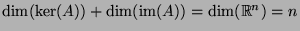 , where
, where
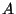 is in fact the linear application associated with
is in fact the linear application associated with 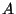 understood as a matrix. By definition,
understood as a matrix. By definition,
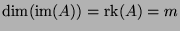 . Thus,
. Thus,
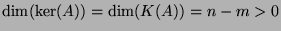 .
.
- 2.
- Let assume that
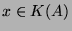 . Then:
Let assume that
. Then:
Let assume that 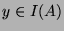 . Then:
We form the inner product to see that it is 0:
That is,
. Then:
We form the inner product to see that it is 0:
That is, 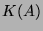 and
and 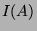 are orthogonal.
are orthogonal.
- 3.
- Both
are reached for
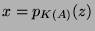 and
and
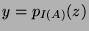 were
were 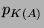 and
and 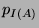 are projections on
are projections on
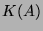 and
and 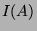 respectively. As
respectively. As
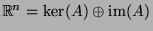 ,
, 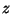 can be written as
can be written as
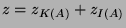 where actually
where actually
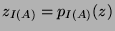 and
and
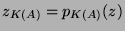 .
.



Next: Information Science I
Up: Mathematics
Previous: Problem 1 - Differentiable
Reynald AFFELDT
2000-06-08
![]() be an
be an
![]() real matrix (
real matrix (![]() ) whose rank is
) whose rank is ![]() . Define
. Define ![]() in the
in the ![]() -dimensional real
vector space
-dimensional real
vector space
![]() as follows:
as follows:
![]() , where
, where
![]() is in fact the linear application associated with
is in fact the linear application associated with ![]() understood as a matrix. By definition,
understood as a matrix. By definition,
![]() . Thus,
. Thus,
![]() .
.