


Next: Problem 4 - Digital
Up: Information Science I
Previous: Information Science I
Prove or disprove the following statements:
- 1.
- Let
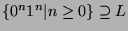 . If
. If 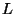 is regular, then
is regular, then 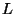 is finite.
is finite.
- 2.
- Let
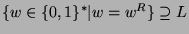 . If
. If 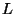 is regular, then
is regular, then 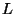 is finite. Here,
is finite. Here,
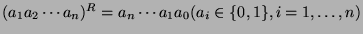 .
.
- 1.
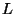 is regular. So,
is regular. So, 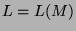 for some finite automaton
for some finite automaton 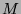 with
with 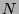 states.
states. 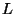 is then infinite if and only
if it accepts some word of length
is then infinite if and only
if it accepts some word of length 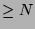 . Let us assume ab absurdo that we have a word
. Let us assume ab absurdo that we have a word 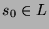 such that
such that
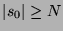 (i.e., we suppose that
(i.e., we suppose that 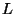 is infinite). The pumping lemma says that we can find
is infinite). The pumping lemma says that we can find
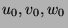 such that
such that
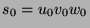 with
with
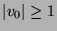 and
and
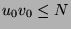 and
and
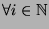 ,
,
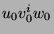 is in
is in 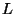 .
. 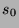 will be of the form
will be of the form 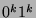 and it means in particular that
and it means in particular that 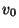 has the form
has the form 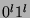 (if it is not the case, it cannot be pumped, and we have a contradiction with the fact that
(if it is not the case, it cannot be pumped, and we have a contradiction with the fact that  is regular).
The pumping lemma then says that
is regular).
The pumping lemma then says that 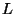 contains the word
contains the word
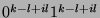 and the number of 0's (together
with the number of
and the number of 0's (together
with the number of 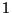 's of course) may grow until it is greater than
's of course) may grow until it is greater than 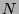 . Let suppose that
. Let suppose that 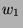 is such
a word. With the same instance of
is such
a word. With the same instance of 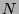 as before, we can find a new decomposition
as before, we can find a new decomposition
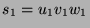 which
satisfies the same criteria. But then it yields a contradiction with the fact that
which
satisfies the same criteria. But then it yields a contradiction with the fact that 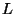 is regular because,
since
is regular because,
since
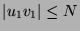 ,
, 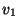 cannot be pumped without yielding a word that is not in
cannot be pumped without yielding a word that is not in 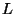 ! We conclude that
such a word
! We conclude that
such a word 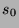 doesn't exist and therefore that
doesn't exist and therefore that 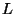 is finite.
is finite.
- 2.
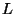 is regular. So,
is regular. So, 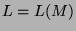 for some finite automaton
for some finite automaton 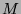 with
with 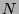 states.
states. 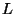 is then infinite if and only
if it accepts some word of length
is then infinite if and only
if it accepts some word of length 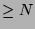 . Let us assume ab absurdo that we have a word
. Let us assume ab absurdo that we have a word 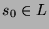 such that
such that
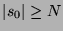 (i.e., we suppose that
(i.e., we suppose that 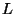 is infinite). The pumping lemma says that we can find
is infinite). The pumping lemma says that we can find
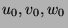 such that
such that
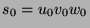 with
with
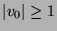 and
and
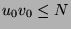 and
and
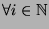 ,
,
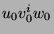 is in
is in 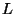 .
. 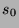 will be a palindrome. Let assume that
will be a palindrome. Let assume that 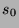 can be noted
can be noted 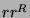 . The fact that
. The fact that 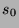 can be
pumped means that
can be
pumped means that 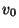 has a even number of symbols which form a symmetric word. We can then pump it
until it reaches a palindrome
has a even number of symbols which form a symmetric word. We can then pump it
until it reaches a palindrome 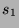 whose length is
whose length is 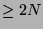 . By applying the pumping lemma with the
. By applying the pumping lemma with the 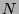 integers, we are given a decomposition for
integers, we are given a decomposition for 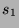 :
: 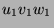 . As
. As
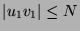 , any attempt to pump
will yield a word that is not a palindrome and therefore is not in
, any attempt to pump
will yield a word that is not a palindrome and therefore is not in 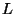 , a contradiction. We conclude
by saying that the assumption that
, a contradiction. We conclude
by saying that the assumption that 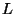 is infinite is absurd.
is infinite is absurd.



Next: Problem 4 - Digital
Up: Information Science I
Previous: Information Science I
Reynald AFFELDT
2000-06-08