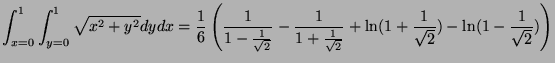![]()
![]()
![]()
![]()
![]()
![]()
![]()
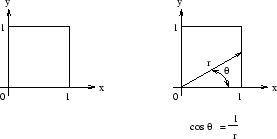
When
![]() , the radius
, the radius ![]() is given by
is given by
![]() . We thus choose
the following change of variables:
. We thus choose
the following change of variables:
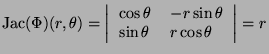
We know that, if
![]() and
and
![]() , we have:
, we have:
![$\displaystyle \int_{[0,1]^2} g(x,y)dxdy = \int_{[0,\sqrt{2}]\times[0,\frac{\pi}{2}]} f(r,\theta)drd\theta$](img1561.png)
Because of the symmetry in ![]() and
and ![]() , we just have to integrate on half of the unit square.
, we just have to integrate on half of the unit square.
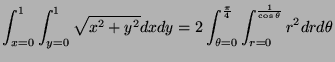
![$\displaystyle = 2 \int_{\theta=0}^{\frac{\pi}{4}} \left[ \frac{r^3}{3}\right]_{r=0}^{\frac{1}{\cos\theta}} d\theta$](img1563.png)
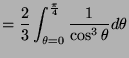
We concentrate on
![]() .
.
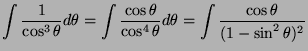
We use the following change of variables:
![]() .
.
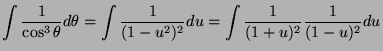
We decompose
![]() into simpler elements:
into simpler elements:
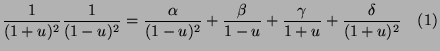
If we form
![]() and then take
and then take ![]() , then
, then
![]() .
.
If we form
![]() and then take
and then take ![]() , then
, then
![]() .
.
If we take ![]() in
in ![]() , then
, then
![]() .
.
If we take ![]() in
in ![]() , then
, then
![]() .
.
That is:
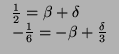
Thus,
![]() .
.
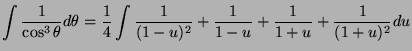
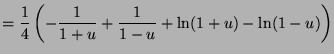
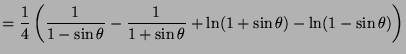
Therefore: