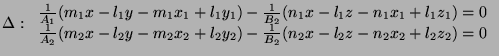The following are two lines in the 3-dimensional ![]() -space which
are assumed to be non-parallel:
-space which
are assumed to be non-parallel:
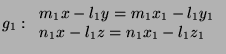
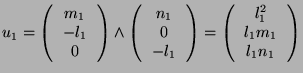
For ![]() :
:
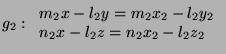
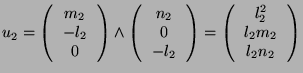
Thus, the following vector indicates the direction of the common perpendicular line:
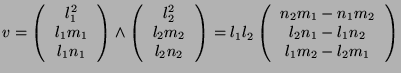
![]() and
and
![]() are respectively parts of
are respectively parts of ![]() and
and ![]() . If we project the
vector
. If we project the
vector
![]() on a normalized
on a normalized ![]() vector, we obtain the minimum distance between
vector, we obtain the minimum distance between ![]() and
and ![]() :
:
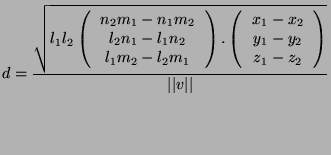
We are seeking for a line ![]() (of direction
(of direction ![]() ) such that it belongs to both a plan
) such that it belongs to both a plan ![]() that contains
that contains
![]() and is orthogonal to
and is orthogonal to ![]() and a plan
and a plan ![]() that contains
that contains ![]() and is orthogonal to
and is orthogonal to ![]() .
.
An equation of ![]() has the following form:
has the following form:
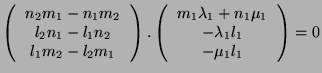
Provided that ![]() and
and ![]() are not equal to 0, we can choose
are not equal to 0, we can choose
![]() and
and
![]() , and we have an equation of the particular
, and we have an equation of the particular ![]() we are looking for.
we are looking for.
Similarly, an equation of ![]() is given by:
is given by:
Then, an equation of the line ![]() is:
is: