


Next: Problem 2 - Determinants
Up: Mathematics
Previous: Mathematics
Answer the following questions about the curve defined by
with a parameter 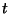
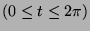 , where
, where 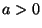 .
.
- 1.
- Draw an outline of this curve.
- 2.
- Compute the area of the region enclosed by the curve.
- 3.
- Compute the length of this curve.
- 1.
- 2.
-
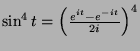
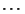

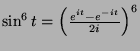
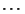
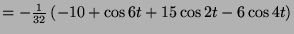
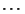
- 3.
-
Reynald AFFELDT
2000-06-08
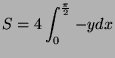
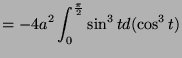
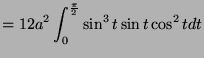
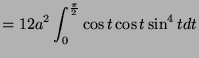
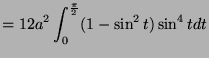
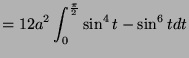
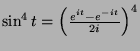
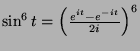
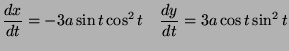
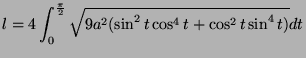
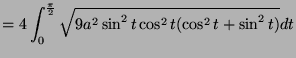
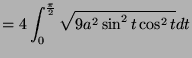
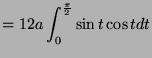
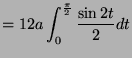
![$\displaystyle = 12a\left[-\frac{1}{4}\cos 2t\right]_{0}^{\frac{\pi}{2}}$](img1719.png)
![$\displaystyle = 12a\left[\frac{1}{4} + \frac{1}{4}\right]$](img1720.png)