
Let


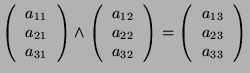
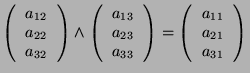
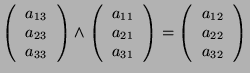
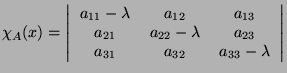
In particular:
From the calculus of the vectorial products in the question above, we can also deduce the
following formulas:
![]()
![]()
We already know that:
![]()
We can therefore eliminate the following terms (in bold below):