


Next: Problem 6 - Compilation
Up: Information Science I
Previous: Problem 4 - Paging
Let us find
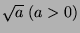 using Newton's method.
using Newton's method.
- 1.
- Give the Newton iteration for the equation
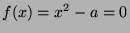 and analyze the convergence behavior of
the
and analyze the convergence behavior of
the 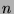 -th approximation
-th approximation 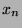 to
to 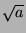 . Assume
. Assume 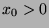 .
.
- 2.
- Give the Newton iteration for the equation
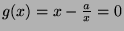 and analyze the convergence
behavior of the
and analyze the convergence
behavior of the 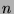 -th approximation
-th approximation 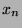 to
to 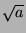 . Assume
. Assume 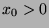 .
.
- 3.
- Let
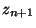 be the arithmetic mean of the
be the arithmetic mean of the 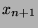 given by the above question 1. and the
given by the above question 1. and the 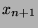 given by the above question 2., assuming the same
given by the above question 2., assuming the same 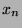 . Analyze the error of
. Analyze the error of 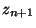 .
.
- 1.
-
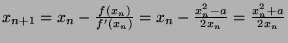
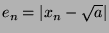
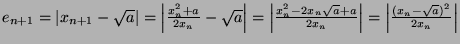
![$ \frac{e_{n+1}}{e_n^2} = \frac{1}{2x_n} \xrightarrow[n\rightarrow +\infty]{} \frac{1}{2\sqrt{a}}$](img1797.png)
Thus, the 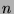 -th approximation converges quadratically.
-th approximation converges quadratically.
- 2.
-
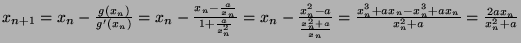
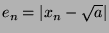
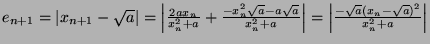
![$ \frac{e_{n+1}}{e_n^2} = \frac{\sqrt{a}}{x_n^2+a} \xrightarrow[n\rightarrow \infty]{} \frac{\sqrt{a}}{2a}$](img1800.png)
Thus, the 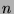 -th approximation converges quadratically.
-th approximation converges quadratically.
- 3.
-
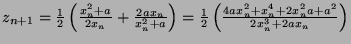
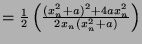
Reynald AFFELDT
2000-06-08
![]() using Newton's method.
using Newton's method.