Next: Problem 7 - Algorithms
Up: Information Science I
Previous: Problem 5 - Numerical
Consider the following pseudo-code (C) and (C'), where the pseudo-code (C') is a code obtained from (C) by
deleting the 5th to 7th lines. mem[x] is a data at address x of memory, call is
a procedure call, ri (i=0,1,2) is a register, and other variables are temporary variables. Suppose
that live variables in the beginning of the code are k and j, and live variables at the
end of the code are d and j. Caller-save registers are r0, r1, r2.
| Pseudo-code (C) |
Pseudo-code (C') |
| |
|
| 1: g <- mem[j+12] |
1: g <- mem[j+12] |
| 2: h <- k - 1 |
2: h <- k - 1 |
| 3: f <- g * h |
3: f <- g * h |
| 4: e <- mem[j+8] |
4: e <- mem[j+8] |
| 5: r0 <- mem[j+16] |
8: b <- mem[f] |
| 6: call proc1 |
9: j <- e + b |
| 7: d <- r0 |
|
| 8: b <- mem[f] |
|
| 9: j <- e + b |
|
- 1.
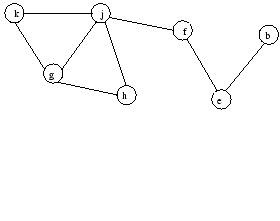
- Concerning the code (C'), construct an undirected graph with nodes corresponding to variables (in the following
a variable and its corresponding node are identified) which satisfies the following condition:
Nodes
x and
y are adjacent
the interval while
x is live and the interval while
y is live intersect.
- 2.
- The
 -coloring problem of a graph is to color each node by using at most
-coloring problem of a graph is to color each node by using at most 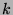 colors so that adjacent nodes
are colored differently, and, when the graph has such a coloring, it is called
colors so that adjacent nodes
are colored differently, and, when the graph has such a coloring, it is called 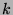 -colorable. If the graph
constructed in the above question is
-colorable. If the graph
constructed in the above question is 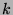 -colorable, the code (C') can be computed using
-colorable, the code (C') can be computed using 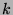 resgiters. Explain
this fact.
resgiters. Explain
this fact.
- 3.
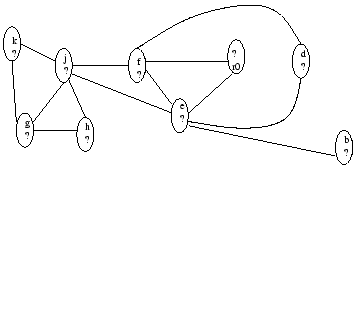
- Construct a graph so that the code (C) can be computed using
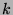 registers if
registers if 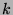 -colorable. The definition
of nodes may be extended if necessary.
-colorable. The definition
of nodes may be extended if necessary.
- 1.
- At the very begining,
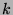 and
and 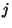 are live. When
are live. When 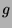 is defined, it is made live while
is defined, it is made live while 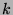 and
and 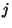 are still
live. But, when
are still
live. But, when 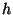 is defined,
is defined, 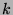 is not live any more. Only
is not live any more. Only 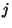 and
and 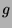 are live.
are live. 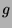 and
and 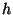 are used
in the determination of
are used
in the determination of 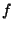 which is made live while
which is made live while 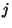 is still live.
is still live. 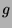 and
and 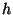 can be dropped out since
they are not used afterwards. The liveness of
can be dropped out since
they are not used afterwards. The liveness of 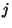 stops when it is used to determine
stops when it is used to determine 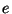 .
. 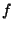 is made dead
when
is made dead
when 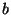 is defined.
is defined. 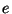 and
and 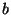 are live together when
are live together when 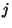 is finally assigned at the last instruction.
is finally assigned at the last instruction.
- 2.
- Let us assume that we have colored the graph with
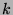 colors. Let
colors. Let 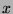 be a variable or its corresponding
node in the graph. When
be a variable or its corresponding
node in the graph. When 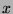 is live, it should be located inside a register. The set of adjacent vertices
of
is live, it should be located inside a register. The set of adjacent vertices
of 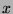 are the variables susceptible to be in a register while
are the variables susceptible to be in a register while 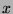 itself is in a register. But not
necessarily all the neighbors of
itself is in a register. But not
necessarily all the neighbors of 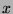 and
and 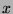 will be in registers at the same time. If
will be in registers at the same time. If 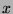 is connected to
is connected to
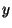 , then
, then 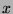 and
and 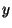 have to share the registers. If
have to share the registers. If 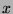 is connected to
is connected to 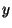 and
and 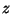 , then
, then 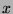 ,
, 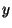 , and
, and
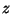 have to share the registers at the same time if and only if
have to share the registers at the same time if and only if 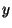 and
and 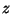 are also connected to each other.
In the latter situation, we see that the coloring of the graph whose set of vertices if
are also connected to each other.
In the latter situation, we see that the coloring of the graph whose set of vertices if 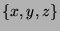 needs
three different colors, but if
needs
three different colors, but if 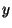 and
and 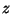 are not connected, then two colors are enough. In similar way,
when all the vertices are live at the same time, three registers should be allocated, instead of only two,
when only two of them are live at the same time. If we associate with each color a register, then the
coloring of the graph tells us how many registers we should use so that at any time all the live variables
can be in registers.
are not connected, then two colors are enough. In similar way,
when all the vertices are live at the same time, three registers should be allocated, instead of only two,
when only two of them are live at the same time. If we associate with each color a register, then the
coloring of the graph tells us how many registers we should use so that at any time all the live variables
can be in registers.
- 3.
- We extend the definition of a node in the following way. A node is either a variable or a register.
A register is said to be 'live' during the time the value that has been affected to him has not been
withdrawn. Once the graph has been constructed, it is colored in such a way that register nodes will
first be affected the demanded color, i.e., the one that corresponds the the register named.



Next: Problem 7 - Algorithms
Up: Information Science I
Previous: Problem 5 - Numerical
Reynald AFFELDT
2000-06-08
 the interval while x is live and the interval while y is live intersect.
the interval while x is live and the interval while y is live intersect.