Problem 7 - Algorithms

Let $A=<a_1,a_2,\dots,a_n>$ be a sequence of integers. Devise a polynomial time algorithm finding a longest increasing subsequence of $A$ (i.e., a longest subsequence $<a_{i_1}, a_{i_2}, \dots, a_{i_k}>$ satisfying $a_{i_j}<a_{i_{j+1}}$ and analyze its time complexity.

Let us assume we have created the following directed graph $G=(V,E)$. The set of vertices is the set of integers. And there is a link from vertex $a_i$ to vertex $a_j$ if and only if $a_j > a_i$. The subsequence we are seeking for is a longest path in this graph. Below stands an instance of such a graph.

$$\includegraphics{increasing-subsequence-of-integers.ps}$$

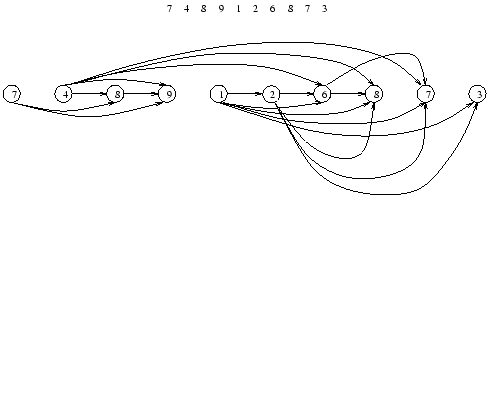
To look for a longest subsequence in such a graph, we can use a val and a dad arrays of $n$ integers. val$[i]$ contains the length a longest path reaching $i$ and dad$[i]$ is its father in such a path. Every time a node is looked at, we check all its successors and we compare their val values with the sum of the val value of the current node plus 1. If the sum is greater then it is assigned to the val entry associated with the successor node and the dad array is updated consequently. The highest val value will denote the last node of a longest path and reading the dad table in reverse order will yield that path.

The algorithm has a $O(n^2)$ time complexity since we have to check each node and for each node the set of its adjacent nodes.