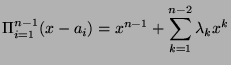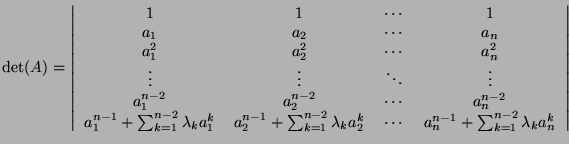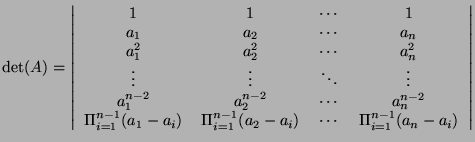Next: Information Science I
Up: Mathematics
Previous: Problem 1 - Wallis
Let
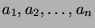 be
be 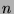 real numbers, and
real numbers, and 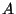 be an
be an
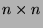 matrix defined by
matrix defined by
- 1.
- Compute the determinant of
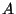 .
.
- 2.
- Give a necessary and sufficient condition that there exists
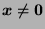 satisfying
satisfying
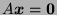 .
.
- 1.
- We shall use the following polynomial:
Without changing the value of the determinant, we can make the following
transformation:
that we can also write as follows:
On the last line, the first
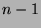 elements are 0 and we are in fact given the following determinant:
We can develop the determinant according to the last line:
where
elements are 0 and we are in fact given the following determinant:
We can develop the determinant according to the last line:
where 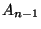 is the same matrix as
is the same matrix as 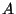 but without the last line and the
rightmost column. We can operate the same transformations on
but without the last line and the
rightmost column. We can operate the same transformations on 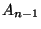 leading to:
Inductively:
that we can also written:
leading to:
Inductively:
that we can also written:
- 2.
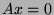 with
with 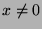 means the linear application that
means the linear application that 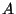 represents is
not a one-to-one mapping and thus
represents is
not a one-to-one mapping and thus 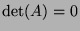 which occurs iff
which occurs iff
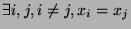 .
.



Next: Information Science I
Up: Mathematics
Previous: Problem 1 - Wallis
Reynald AFFELDT
2000-06-08
![]() be
be ![]() real numbers, and
real numbers, and ![]() be an
be an
![]() matrix defined by
matrix defined by