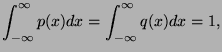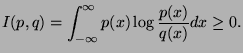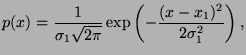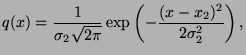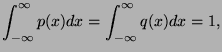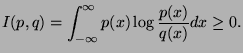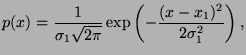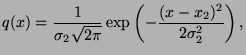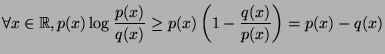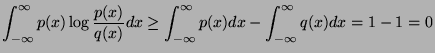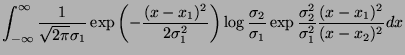Next: Problem 2 - Algebra
Up: Mathematics
Previous: Mathematics
- 1.
- For
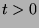 , prove
, prove
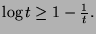
- 2.
- For functions
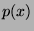 ,
, 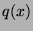 defined over
defined over
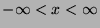 such that
prove the following equality holds:
such that
prove the following equality holds:
- 3.
- For functions
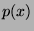 and
and 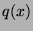 defined by
compute
defined by
compute 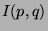 . Here,
. Here,
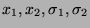 are constants.
are constants.
- 1.
- For
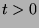 , we study the function defined by
, we study the function defined by
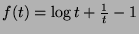 whose first derivative
is
whose first derivative
is
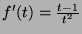 . This function is
. This function is 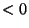 for
for 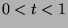 and
and 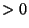 for
for 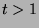 . This means,
. This means, 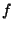 is
decreasing on the way to 1 and increasing afterwards. It reaches its minimum in 1 and this minimum has 0
as a value. From this, we conclude
is
decreasing on the way to 1 and increasing afterwards. It reaches its minimum in 1 and this minimum has 0
as a value. From this, we conclude
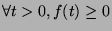 which is equivalent to the statement we're
asked about.
which is equivalent to the statement we're
asked about.
- 2.
-
We integrate the inequality and get:
since
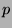 and
and 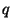 are probability density functions.
are probability density functions.
- 3.
-
TODO: What am I suppose to find?
Reynald AFFELDT
2000-06-08