


Next: Information Science I
Up: Mathematics
Previous: Problem 1 - Probability
For subspaces 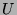 ,
, 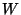 of
of 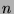 -dimensional real vector space
-dimensional real vector space 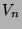 , define
, define
 ,
, 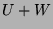 by
by
- 1.
- Show that
 and
and 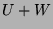 are real vector spaces.
are real vector spaces.
- 2.
- Suppose that
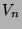 is the 3-dimensional space with
is the 3-dimensional space with 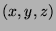 -coordinate.
-coordinate.
- (a)
- When
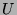 is the
is the 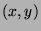 -plane and
-plane and 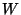 is the
is the 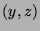 -plane, whate are
-plane, whate are
 ,
, 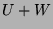 ? Also, give the dimensions of
? Also, give the dimensions of  and
and 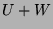 .
.
- (b)
- When
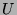 is the
is the 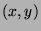 -plane and
-plane and 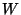 is the
is the 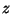 -axis, whate are
-axis, whate are  ,
, 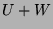 ? Also, give the dimensions of
? Also, give the dimensions of  and
and 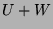 .
.
- 3.
- Denote the dimension of real vector space
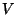 by
by 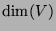 . Prove the
following equality:
. Prove the
following equality:
- 1.
 and
and 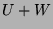 are they real vector spaces?
are they real vector spaces?
- (a)
 is a real vector space because:
is a real vector space because:
- i.
 is an abelian group because:
is an abelian group because:
- a.
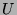 and
and 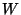 are subspaces, therefore
are subspaces, therefore
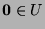 and
and
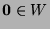 , therefore
, therefore
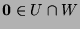 ;
;
- b.
-
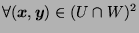 ,
,
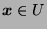 and
and
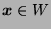 and
and
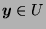 and
and
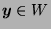 , therefore
, therefore
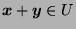 and
and
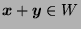 (since
(since 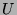 and
and 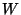 are vector
spaces), therefore
are vector
spaces), therefore
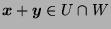 ;
;
- c.
-
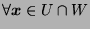 ,
,
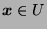 and
and
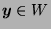 , therefore
, therefore
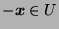 and
and
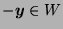 (since
(since 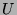 and
and 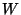 are vector spaces), therefore
are vector spaces), therefore
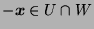 .
.
- ii.
-
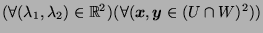 we have (since these
properties are already true for both
we have (since these
properties are already true for both 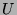 and
and 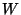 ):
):
- a.
-
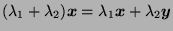 ;
;
- b.
-
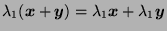 .
.
- iii.
-
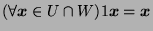 (since this property is already true for both
(since this property is already true for both 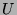 and
and 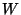 ).
).
- iv.
-
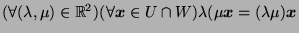 (since
these property is already true for both
(since
these property is already true for both 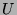 and
and 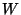 ).
).
- (b)
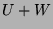 is also a real vector space for the same reasons.
is also a real vector space for the same reasons.
This is raw check of the definition of a vector space. It is better to apply
the theorem saying that a set included in a vector space is a subspace iff it
is stable for the addition and for the scalar multiplication.
- 2.
- Can you explicit
 and
and 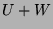 and their dimensions in a
practical case study?
and their dimensions in a
practical case study?
- (a)
- i.
-
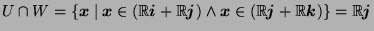 because
because
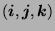 is a set of basis vectors. Therefore,
is a set of basis vectors. Therefore,
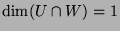 .
.
- ii.
-
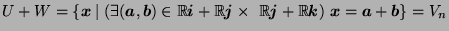 . Therefore,
. Therefore,
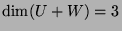 .
.
- (b)
- i.
-
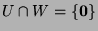 and
and
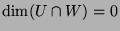 .
.
- ii.
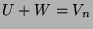 and
and
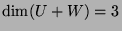 .
.
- 3.
- Can you show that
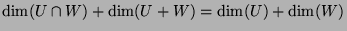 ?
?
Let us consider the application
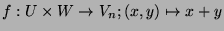 .
.
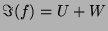 .
.
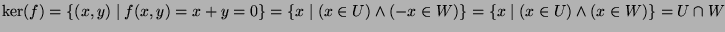 (remember that W is a vector space). The rank formula gives us
the following equality:
(remember that W is a vector space). The rank formula gives us
the following equality:
Since we know that
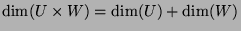 , we have shown
that the following equality holds:
, we have shown
that the following equality holds:



Next: Information Science I
Up: Mathematics
Previous: Problem 1 - Probability
Reynald AFFELDT
2000-06-08
![]() ,
, ![]() of
of ![]() -dimensional real vector space
-dimensional real vector space ![]() , define
, define
![]() ,
, ![]() by
by
![]() .
.
![]() .
.
![]() (remember that W is a vector space). The rank formula gives us
the following equality:
(remember that W is a vector space). The rank formula gives us
the following equality: