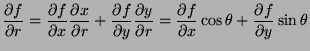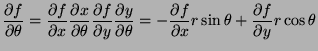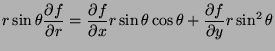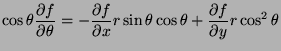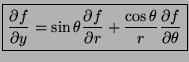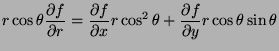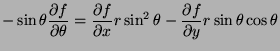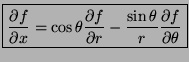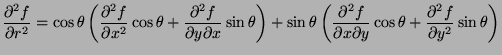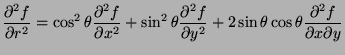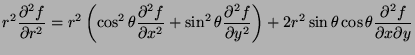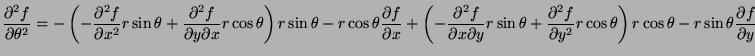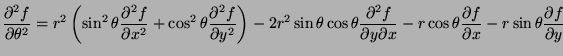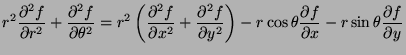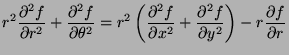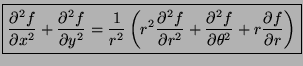Next: Problem 2 - Determinants
Up: Mathematics
Previous: Mathematics
Concerning the transformation between the orthogonal coordinates and polar coordinates, answer the following
questions.
- 1.
- Represent
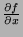 and
and
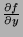 in terms of
in terms of
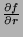 and
and
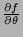 .
.
- 2.
- Represent
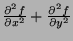 in terms of the partial
derivatives of
in terms of the partial
derivatives of 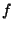 with respect to
with respect to 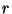 and
and 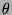 .
.
- 1.
-
- 2.
-
Reynald AFFELDT
2000-06-08