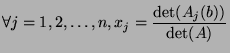We shall show by induction on the size of the (square) matrix 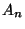 that
that
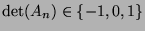 .
.
This is obvious for  . For
. For  , the determinant of
, the determinant of 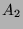 will be of the form
will be of the form 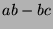 if the matrix is
denoted:
if the matrix is
denoted:
As the elements can be only 0 or 1,
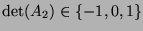 .
.
Let us now assume that this property is true for 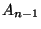 and let us consider any
and let us consider any 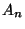 matrix satisfying the
definition above. We consider the first line of this matrix.
matrix satisfying the
definition above. We consider the first line of this matrix.
- If this line is filled with 0's, then
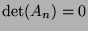 .
.
- If this line is filled with 0's except for the first element which is a 1, we can develop the determinant
so that
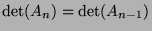 , which belongs to
, which belongs to
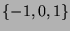 according to the inductive hypothesis.
according to the inductive hypothesis.
- If this line is randomly filled with 0's and 1's, we can make operations on some columns with other
columns (addition, subtraction) so that after a finite number of operations we find ourselves in the previous
case without changing the value of the determinant of
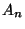 .
.
Thus, we have inductively proven that
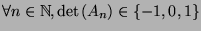 .
.
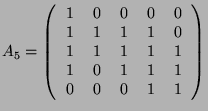
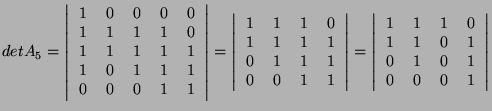
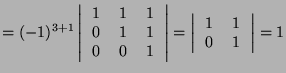
![]() . For
. For ![]() , the determinant of
, the determinant of ![]() will be of the form
will be of the form ![]() if the matrix is
denoted:
if the matrix is
denoted:
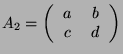
![]() and let us consider any
and let us consider any ![]() matrix satisfying the
definition above. We consider the first line of this matrix.
matrix satisfying the
definition above. We consider the first line of this matrix.