Problem 1 - Vector Spaces

1.

Let $x_1$, $x_2$ be two linearly independent vectors in the 2-dimensional real vector space, and define $y_1$, $y_2$ by

$$y_1 = \frac{x_1}{\vert\vert x_1\vert\vert},$$

$$y_2 = \frac{x_2 - (y_1,x_2)y_1}{\vert\vert x_2 - (y_1,x_2)y_1\vert\vert}.$$

Here, $(x,y)$ is the inner product of $x$ and $y$, and $\vert\vert x\vert\vert=\sqrt{(x,x)}$. Prove that $y_1$ and $y_2$ are orthogonal.

2.

Let $x_1$, ..., $x_n$ be $n$ linearly independent vectors in the $n$-dimensional real vector space. Give a method of constructing a normalized orthogonal system represented by linear combinations of these vectors, together with its validity.

1.

$$(y_1,y_2)=\frac{1}{\vert\vert x_1\vert\vert}\frac{1}{\vert\vert x_2-(y_1,x_2)y_1\vert\vert}\left(x_1,x_2-(y_1,x_2)y_1)\right)$$

$$=\frac{1}{\vert\vert x_1\vert\vert}\frac{1}{\vert\vert x_2-(y_1,x_2)y_1\vert\vert}\left((x_1,x_2)-(x_1,(y_1,x_2)y_1)\right)$$

$$=\frac{1}{\vert\vert x_1\vert\vert}\frac{1}{\vert\vert x_2-(y_1,x_2)y_1\vert\vert}\left((x_1,x_2)-(y_1,x_2)(x_1,y_1)\right)$$

$$=\frac{1}{\vert\vert x_1\vert\vert}\frac{1}{\vert\vert x_2-(y_1,x... ...t}\left((x_1,x_2)-\frac{1}{\vert\vert x_1\vert\vert^2}(x_1,x_2)(x_1,x_1)\right)$$

$$=\frac{1}{\vert\vert x_1\vert\vert}\frac{1}{\vert\vert x_2-(y_1,x... ...-\frac{1}{\vert\vert x_1\vert\vert^2}(x_1,x_2)\vert\vert x_1\vert\vert^2\right)$$

$$=\frac{1}{\vert\vert x_1\vert\vert}\frac{1}{\vert\vert x_2-(y_1,x_2)y_1\vert\vert}\left((x_1,x_2)-(x_1,x_2)\right)$$

$$=0$$

Thus, $y_1$ and $y_2$ are orthogonal.

2.

We can use the following construct of a orthonormalized base:
$y_1 = \frac{x_1}{\vert\vert x_1\vert\vert}$
$y_2 = \frac{x_2 - (y_1,x_2)y_1)}{\vert\vert x_2 - (y_1,x_2)y_1)\vert\vert}$
$y_3 = \frac{x_3 - (y_2,x_3)y_2 - (y_1,x_3)y_1)}{\vert\vert x_3 - (y_2,x_3)y_2 - (y_1,x_3)y_1\vert\vert}$
$\cdots$
$y_n = \frac{x_n - \sum_{i=1}^{n-1}(y_i,y_n)y_i}{\vert\vert x_n - \sum_{i=1}^{n-1}(y_i,y_n)y_i\vert\vert}$

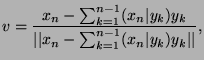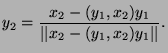
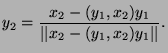
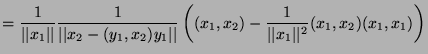
The theorem would state that given any sequence of $n$ linearly independent vectors $x_i$, there is one and only one sequence of orthonormal vectors $y_i$ such that:

$$\forall k\in[1,n], \quad Vect(x_1,\dots,x_k)=Vect(y_1,\dots,y_k)\quad\hbox{and}\quad(x_k\vert y_k)>0$$

Let us prove it by induction on $n$, the number of initial linearly vectors.

If $n=1$, the theorem is obvious and the single vector sought is $y_1 = \frac{x_1}{\vert\vert x_1\vert\vert}$.

We now suppse the theorem is true for $n-1\geq 1$. We consider an initial sequence of $n$ linearly independent vectors $x_i$. By the inductive hypothesis we already have a sequence of vectors $y_i$ such that:

$$\forall k\in[1,n-1], \quad Vect(x_1,\dots,x_k)=Vect(y_1,\dots,y_k)\quad\hbox{and}\quad(x_k\vert y_k)>0$$

If there is a sequence of $n$ orthornormalized vectors $y_i'$ such that:

$$\forall k\in[1,n], \quad Vect(x_1,\dots,x_k)=Vect(y_1',\dots,y_k')\quad\hbox{and}\quad(x_k\vert y_k')>0$$

then, because the sequence is for each $k$ unique, we have $\forall k\in[1,n-1], y_k'=y_k$. That's why we just have to show that $y_n$ satisfies also the requirements.

Analysis: If such a $y_n$ exist, then $y_n\in Vect(x_1,\dots,x_n)=Vect(y_1,\dots,y_{n-1},x_n)$. Therefore,

$$y_n = \lambda x_n + \sum_{k=1}^{n-1}\alpha_k y_k$$

where $\lambda, \alpha_i \in \mathbb{R}$. $\forall i\in[1,n-1], (y_n,y_i)=0$ thus:

$$0=\lambda (x_n,y_i) + \sum_{k=1}^{n-1}\alpha_k (y_k,y_i) = \lambda(x_n,y_i) + \alpha_i,$$

so that

$$y_n = \lambda \left(x_n - \sum_{k=1}^{n-1}(x_n,y_i)y_i\right)$$

Moreover, $\vert\vert y_n\vert\vert=1=\vert\lambda\vert\vert\vert x_n - \sum_{k=1}^{n-1}(x_n,y_i)y_i\vert\vert$ and this gives the value of $\lambda$. If we take $\lambda \in \mathbb{R}_+^*$, then the last requirement $(y_n,x_n)>0$ is also verified.

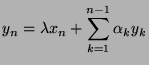
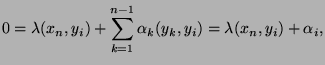
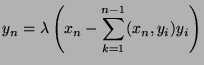
Synthesis: If we just take a closer look at:

$$v = \frac{x_n - \sum_{k=1}^{n-1}(x_n\vert y_k)y_k}{\vert\vert x_n - \sum_{k=1}^{n-1}(x_n\vert y_k)y_k\vert\vert},$$

we notice it verifies all the requirements.