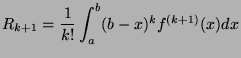Next: Information Science I
Up: Mathematics
Previous: Problem 1 - Vector
For a function 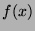 on the closed interval
on the closed interval ![$ [a,b]$](img509.png) which is differentiable
which is differentiable 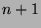 times, there exists the
Taylor expansion
times, there exists the
Taylor expansion
- 1.
- Compute
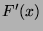 for
for
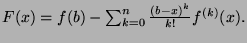
- 2.
- Show
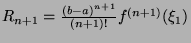 ,
,
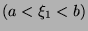 .
.
- 3.
- Show
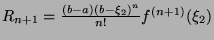 ,
,
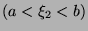 .
.
- 4.
- Prove, by induction concerning
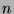 ,
,
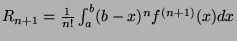 .
.
- 1.
-
- 2.
- We first notice that
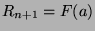 . Let us assume that we are given the following function:
We have both
. Let us assume that we are given the following function:
We have both 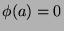 and
and 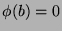 (because
(because 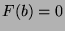 ). Thus, by the Rolle theorem,
). Thus, by the Rolle theorem,
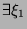 such
that
such
that 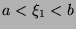 and
and
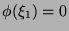 .
.
- 3.
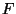 is differentiable because
is differentiable because 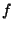 is
is 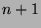 times differentiable, which means
times differentiable, which means
![$ \exists \xi_2 \in ]a,b[$](img535.png) such that:
such that:
- 4.
- For
 , we have by definition
, we have by definition
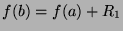 and
and
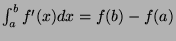 , and the property is true
for
, and the property is true
for  .
Let us assume that the property is true for
.
Let us assume that the property is true for 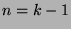 , i.e. we have:
By definition, we have:
which is merely the decomposition of the following integral:
Therfore:
and the property has been proved by induction.
, i.e. we have:
By definition, we have:
which is merely the decomposition of the following integral:
Therfore:
and the property has been proved by induction.



Next: Information Science I
Up: Mathematics
Previous: Problem 1 - Vector
Reynald AFFELDT
2000-06-08
![]() on the closed interval
on the closed interval ![]() which is differentiable
which is differentiable ![]() times, there exists the
Taylor expansion
times, there exists the
Taylor expansion
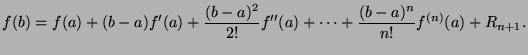
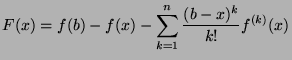
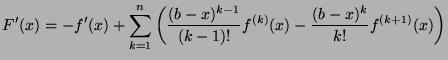
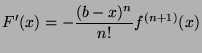
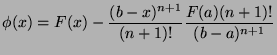
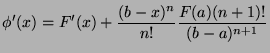
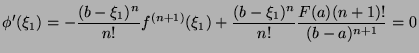
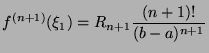
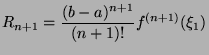
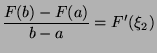
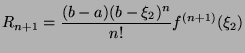
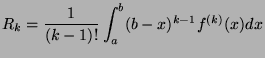
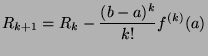
![$\displaystyle \frac{1}{k!}\int_a^b (b-x)^kf^{(k+1)}(x)dx = \frac{1}{k!}\left( \left[(b-x)^kf^{(k)}(x)\right]_a^b + \int_a^b n(b-x)^{k-1}f^{(k)}dx\right)$](img544.png)