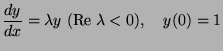
The precision and stability of numerical methods for differential equation are investigated by using
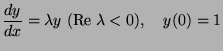
as an example problem. For each of the three methods below, compute errors in the first step and find a condition (stability condition) so that the following holds:
where ![]() is a numerical solution for
is a numerical solution for ![]() .
.
|
|
|
|
|
|
||
|
|
The stability condition is determined by:
![]()
Which is true if:
|
|
|
|
|
|
|
Which means
![]()
|
|
|
|
|
|
||
|
|
||
|
|
The stability condition is determined by:
![]()
Since:
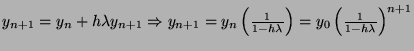
It is satisfied for:
|
|
|
|
|
|
|
Which means
![]() .
.
|
|
|
|
|
|
||
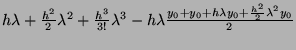 |
||
|
|
||
|
|
The stability condition is determined by:
![]()
Since:
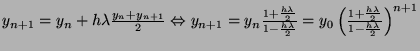
It is satisfied for:
|
|
|
|
|
|
|
|
|
|
|
Which is always true since
![]() and
and
![]() .
.