Consider a context-free grammar with the following production rules, where ![]() denotes an empty string.
Terminals symbols are
denotes an empty string.
Terminals symbols are
![]() ,
, ![]() ,
, ![]() and parentheses.
and parentheses.
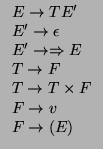
![$\displaystyle \begin{tabular}{l}
$M[E',)]$ \\
$M[E',\Rightarrow]$ \\
$M[E',...
... \\
$M[T',)]$ \\
$M[T',\Rightarrow]$ \\
$M[T',\times]$ \\
\end{tabular}$](img617.png)
Then, we build fonction FOLLOW for every non-terminal.
First, since ![]() is the axiom, we had $ to FOLLOW
is the axiom, we had $ to FOLLOW
![]() .
.
Then, we look at all the production
![]() , and we add the contents of FIRST
, and we add the contents of FIRST![]() (except
(except
![]() ) to FOLLOW
) to FOLLOW![]() .
.
Since
![]() , FOLLOW
, FOLLOW
![]() .
.
Since
![]() , FOLLOW
, FOLLOW
![]() .
.
Since
![]() , FOLLOW
, FOLLOW
![]() .
.
Finally, we look at all the productions
![]() (or
(or
![]() with
with
![]() ) and we add FOLLOW
) and we add FOLLOW![]() to FOLLOW
to FOLLOW![]() .
.
Since
![]() , FOLLOW
, FOLLOW
![]() and FOLLOW
and FOLLOW
![]() .
.
Since
![]() , FOLLOW
, FOLLOW
![]() .
.
Since
![]() , FOLLOW
, FOLLOW
![]() and FOLLOW
and FOLLOW
![]() .
.
As these sets are closed, we conclude:
FOLLOW
![]()
FOLLOW
![]()
FOLLOW
![]()
FOLLOW
![]()
FOLLOW
![]()
Now, we build the predictive parse table. For each production
![]() , we do the following. For each terminal
, we do the following. For each terminal ![]() in FIRST
in FIRST![]() , we add
, we add
![]() to
to ![]() . If
. If ![]() is in FIRST
is in FIRST![]() , we add
, we add
![]() to
to ![]() for all the terminals in FOLLOW
for all the terminals in FOLLOW![]() . If
. If ![]() is in FIRST
is in FIRST![]() and $ is in FOLLOW(A), we had
and $ is in FOLLOW(A), we had
![]() to
to ![]() .
.
We add
![]() to
to
![]() .
.
We add
![]() to
to
![]() .
.
We add
![]() to
to ![]() and
and ![]() .
.
We add
![]() to
to
![]() ,
, ![]() and
and ![]() .
.
No productions involving ![]() as a left-hand yields an entry to
as a left-hand yields an entry to
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
The ![]() locates errors in the parse table.
locates errors in the parse table.