Problem 3 - Compilation

Answer the following questions about the context-free grammar defined below.

$$S \rightarrow a \; \vert \; a ; S \; \vert \; \textbf{begin} \; S \; \textbf{end}$$

The symbols $a$, ;, begin, and end are assumed to be terminals.

1.

Explain why this grammar is not LL(1).

2.

Show that this grammar is SLR(1).

1.

Obviously, this grammar is not not LL(1) since, when seeing an $a$, the predictive parser cannot know which production to use. There is a multiple choice in the associated parse table. Therefore, it cannot be the parse table of a LL(1) grammar.

2.

We build the SLR(1) parse table for the given grammar.
We consider the following grammar:
$S\rightarrow a$
$S\rightarrow a\;;\;S$
$S\rightarrow \hbox{begin}\;S\;\hbox{end}$

We will work with the following augmented grammar:
$S'\rightarrow S$
$S\rightarrow a$
$S\rightarrow a\;;\;S$
$S\rightarrow \hbox{begin}\;S\;\hbox{end}$

First, we build $C=\{I_0, I_1, \dots\}$, the collection of $LR(0)$ items for the augmented grammar: (the third column will be explained later)

$I_0$	$S'\rightarrow .S$	$Next[0,S]=1$
	$S\rightarrow .a$	$Action[0,a]=s2$
	$S\rightarrow .a;S$	$Action[0,a]=s2$
	$S\rightarrow . \hbox{begin}\;S\;\hbox{end}$	$Action[0,\hbox{begin}]=s3$
$I_1$	$S'\rightarrow S.$	$Action[1,\$]=accept$
$I_2$	$S\rightarrow a.$	$Action[2,\{\$,\hbox{end},;\}]=r\;S\rightarrow a$
	$S\rightarrow a.;S$	$Action[2,;]=s4$
$I_3$	$S\rightarrow\hbox{begin}.S\;\hbox{end}$	$Next[3,S]=5$
	$S\rightarrow .a$	$Action[3,a]=s2$
	$S\rightarrow .a;S$	$Action[3,a]=s2$
	$S\rightarrow . \hbox{begin}\;S\;\hbox{end}$	$Action[3,\hbox{begin}]=s3$
$I_4$	$S\rightarrow a;.S$	$Next[4,S]=6$
	$S\rightarrow .a$	$Action[4,a]=s2$
	$S\rightarrow .a;S$	$Action[4,a]=s2$
	$S\rightarrow . \hbox{begin}\;S\;\hbox{end}$	$Action[4,\hbox{begin}]=s3$
$I_5$	$S\rightarrow\hbox{begin}\;S.\hbox{end}$	$Action[5,\hbox{end}]=s7$
$I_6$	$S\rightarrow a;S.$	$Action[6,\{\$,\hbox{end}\}]=r\;S\rightarrow a;S$
$I_7$	$S\rightarrow\hbox{begin}\;S\;\hbox{end}.$	$Action[7,\{\$,\hbox{end}\}]=r\;S\rightarrow\hbox{begin}\;S\;\hbox{end}$

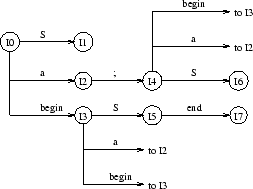
Then, we fill up the 'Action' part of the parse table, that is the part of the table from which, given a state $s_m$ and an input symbol $a_i$, we will be able to know if we have to shift the input symbol and with which state or if we have to reduce thanks to a particular production. In this last case, we push on the stack the left-hand of the production with a state given by the 'Next' part of the parse table (part that we will build afterwards). The state $i$ is built from $I_i$. The analysis actions for the state $i$ are determined as follows:

• If $[A\rightarrow \alpha . a \beta]$ is in $I_i$ and $Goto(I_i,a)=I_j$, then we fil $Action[i,a]$ with 'shift $j$'. Here, $a$ must be a terminal.
• If $[A\rightarrow \alpha .]$ is in $I_i$, we fill $Action[i,a]$ with 'reduce thanks to $A\rightarrow \alpha$' for all the $a$ in FOLLOW($A$); here, $A$ cannot be $S'$.
• If $S'\rightarrow S.$ is in $I_i$, then we fill $Action[i,\$]$ with 'accept'.

If there is no conflict, the grammar is SLR(1). For conveniency, we indicate the results in the table of the canonial items above.

We need the following sets:
FOLLOW $(S)=\{\$,\hbox{end}\}$
FOLLOW $(a)=\{\$,\hbox{end},;\}$
FOLLOW $(\hbox{end}=\{\$,\hbox{end}\}$

For $S\rightarrow a.$ in $I_2$, we have $Action[2,\{\$,\hbox{end},;\}]$ filled with 'reduce with $S\rightarrow a$'. For $S\rightarrow a;S.$ in $I_6$, we have $Action[4,\{\$,\hbox{end}\}]$ filled with 'reduce with $S\rightarrow a;S$'.

For $S\rightarrow\hbox{begin}\;S\;\hbox{end}.$ in $I_7$, we have $Action[7,\{\$,\hbox{end}\}]$ filled with 'reduce with $S\rightarrow \hbox{begin}\;S\;\hbox{end}$'.

Then we build the 'Next' part of the parse table. For state $i$ and for any non-terminal $A$, we have, if $Goto(I_i,A)=I_j$, alors $Next[i,A]=j$.

This grammar becomes SLR(1) if we eliminate the conflict for ';' in $I_2$ by eliminating it from FOLLOW$(a)$.