For ![]() -dimensional vectors
-dimensional vectors ![]() ,
,![]()
![]() of the same length, an
of the same length, an ![]() matrix
matrix ![]() defined by
defined by
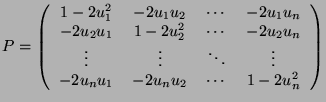
Let
![]() be a line of
be a line of ![]() and
and
![]() be a column of
be a column of ![]() . The
. The ![]() th element
of
th element
of
![]() is equal to
is equal to ![]() if
if ![]() and to
and to ![]() if
if ![]() . The
. The ![]() th
element of
th
element of
![]() is equal to
is equal to ![]() if
if ![]() and to
and to ![]() if
if ![]() .
.
Suppose we look for an element ![]() of the matrix
of the matrix ![]() . This element is:
. This element is:
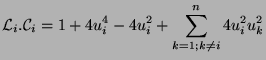
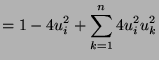
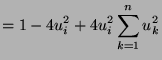
Now, we look for an element ![]()
![]() of the matric
of the matric ![]() . This element is:
. This element is:
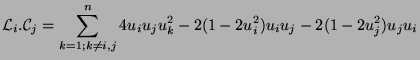
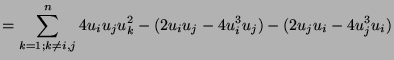
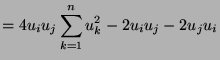
And thus ![]() and
and ![]() is orthogonal.
is orthogonal.