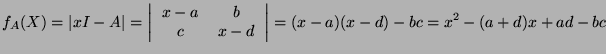Next: Problem 2 - Differential
Up: Mathematics
Previous: Mathematics
For a
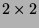 matrix
matrix
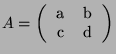 , answer
the following questions.
, answer
the following questions.
- 1.
- Compute the characteristic polynomial
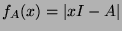 , where
, where 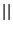 is the determinant of a matrix, and
is the determinant of a matrix, and
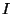 is a
is a
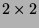 unit matrix.
unit matrix.
- 2.
- Compute
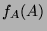 .
.
- 3.
- A polynomial
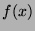 is called a minimal polynomial of
is called a minimal polynomial of 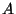 if
if 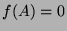 , its coefficients are scalar,
the coefficient of highest degree is 1, and the degree is minimum with respect to these properties. The minimal
polynomial of
, its coefficients are scalar,
the coefficient of highest degree is 1, and the degree is minimum with respect to these properties. The minimal
polynomial of 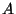 is denoted by
is denoted by 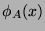 . Show that
. Show that
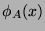 divides
divides 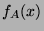 .
.
- 4.
- For an eigenvalue
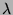 of
of 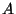 , show
, show
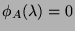 .
.
- 1.
-
- 2.
-
- 3.
-
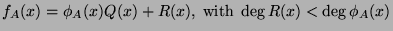 .
.
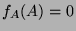 and
and
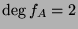 .
.
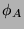 is a minimal degree polynomial such that it has a zero value when applied to
is a minimal degree polynomial such that it has a zero value when applied to 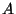 .
.
It means that
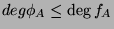 .
.
Let us first assume that
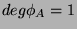 .
.
Then it means that
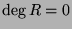 .
.
Then, since
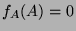 , it implies that
, it implies that 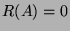 , and finally
, and finally  .
.
Thus, 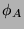 divides
divides 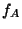 .
.
Let us now assume that
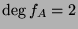 .
.
Then it means that
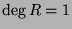 .
.
For instance,
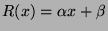 .
.
Since, 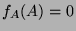 , then
, then 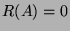 .
.
Thus, 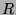 is a polynomial that has a zero value in
is a polynomial that has a zero value in 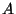 and whose degree
and whose degree
is inferior to the one of 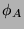 , which is not possible by definition.
, which is not possible by definition.
Therefore,
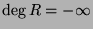 and
and 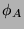 divides
divides 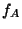 .
.
- 4.
- Let
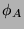 be
be
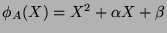 .
.
We have
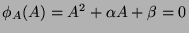 .
.
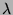 is an eigenvalue of
is an eigenvalue of 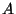 . Thus
. Thus
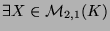 so that:
so that:
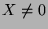 and
and
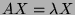 ,
,
 , etc.
, etc.
Therefore,
![$ \phi_A(A)[X] = \lambda^2 X + \alpha \lambda X + \beta X = \left( \phi_A(\lambda) \right) X$](img954.png) .
.
Since
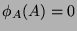 and
and 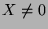 , we have
, we have
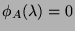 .
.



Next: Problem 2 - Differential
Up: Mathematics
Previous: Mathematics
Reynald AFFELDT
2000-06-08
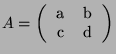 , answer
the following questions.
, answer
the following questions.
![]() matrix
matrix
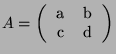 , answer
the following questions.
, answer
the following questions.