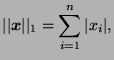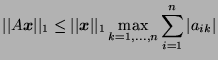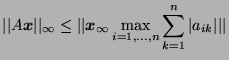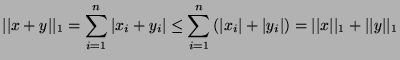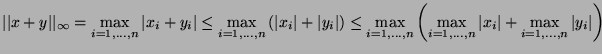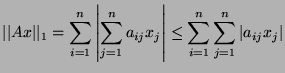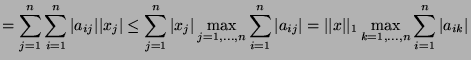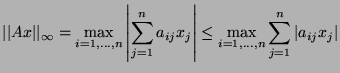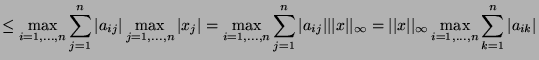Problem 1 - Norms

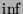$1$-norm and $\inf$-norm of a real 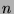$n$-component vector are defined as follows:

$$\vert\vert\boldsymbol{x}\vert\vert _1 = \sum_{i=1}^n \vert x_i\vert,$$

$$\vert\vert\boldsymbol{x}\vert\vert _{\infty} = \max_{i=1, \dots, n} \vert x_i\vert.$$

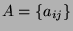Let $A = \{ a_{ij} \}$ be a real square matrix of order 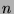$n$. Answer the following questions.

1.

Prove the following triangular inequalities:

$$\vert\vert\boldsymbol{x}+\boldsymbol{y}\vert\vert _1 \leq \vert\vert\boldsymbol{x}\vert\vert _1 + \vert\vert\boldsymbol{y}\vert\vert _1,$$

$$\vert\vert\boldsymbol{x}+\boldsymbol{y}\vert\vert _{\infty} \leq ... ...ldsymbol{x}\vert\vert _{\infty} + \vert\vert\boldsymbol{y}\vert\vert _{\infty}.$$

2.

Show

$$\vert\vert A\boldsymbol{x}\vert\vert _1 \leq \vert\vert\boldsymbol{x}\vert\vert _1 \max_{k=1,\dots,n} \sum_{i=1}^n \vert a_{ik}\vert$$

3.

For a given 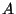$A$, give an example of 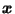$\boldsymbol{x}$ for which the equal sign holds in the previous inequality.

4.

Show

$$\vert\vert A\boldsymbol{x}\vert\vert _{\infty} \leq \vert\vert\boldsymbol{x}_{\infty} \max_{i=1,\dots,n} \sum_{k=1}^n \vert a_{ik}\vert\vert\vert$$

5.

For a given 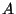$A$, give an example of 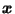$\boldsymbol{x}$ for which the equal sign holds in the previous inequality.

1.

$$\vert\vert x+y\vert\vert _1 = \sum_{i=1}^n \vert x_i + y_i\vert \... ...+\vert y_i\vert \right) = \vert\vert x\vert\vert _1 + \vert\vert y\vert\vert _1$$

$$\vert\vert x+y\vert\vert _\infty = \max_{i=1,\dots,n} \vert x_i +... ...eft( \max_{i=1,\dots,n}\vert x_i\vert + \max_{i=1,\dots,n}\vert y_i\vert\right)$$

$$=\max_{i=1,\dots,n}\vert x_i\vert + \max_{i=1,\dots,n}\vert y_i\vert = \vert\vert x\vert\vert _\infty + \vert\vert y\vert\vert _\infty$$

2.

$$\vert\vert Ax\vert\vert _1 = \sum_{i=1}^n \left\vert \sum_{j=1}^n a_{ij}x_j\right\vert \leq \sum_{i=1}^n \sum_{j=1}^n \vert a_{ij}x_j\vert$$

$$= \sum_{j=1}^n \sum_{i=1}^n\vert a_{ij}\vert\vert x_j\vert \leq \... ...rt = \vert\vert x\vert\vert _1 \max_{k=1,\dots,n}\sum_{i=1}^n \vert a_{ik}\vert$$

3.

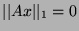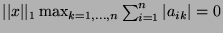With $x=0$, $\vert\vert Ax\vert\vert _1 = 0$ and $\vert\vert x\vert\vert _1\max_{k=1,\dots,n}\sum_{i=1}^n\vert a_{ik}\vert = 0$, and the equality in 2. holds.

4.

$$\vert\vert Ax\vert\vert _\infty = \max_{i=1,\dots,n}\left\vert \s... ... a_{ij}x_j\right\vert \leq \max_{i=1,\dots,n} \sum_{j=1}^n \vert a_{ij}x_j\vert$$

$$\leq \max_{i=1,\dots,n} \sum_{j=1}^n \vert a_{ij}\vert\max_{j=1,\... ...vert\vert x\vert\vert _\infty \max_{i=1,\dots,n} \sum_{k=1}^n \vert a_{ik}\vert$$

5.

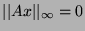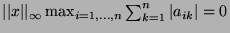With $x=0$, $\vert\vert Ax\vert\vert _\infty = 0$ and $\vert\vert x\vert\vert _\infty\max_{i=1,\dots,n}\sum_{k=1}^n\vert a_{ik}\vert = 0$, and the equality in 4. holds.