


Next: Information Science I
Up: Mathematics
Previous: Problem 1 - Norms
For an integer 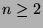 , define
, define 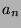 by
by
where 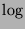 is the natural logarithm and
is the natural logarithm and 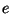 below is the base of the
natural logarithm.
below is the base of the
natural logarithm.
- 1.
- Show
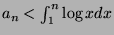 .
.
- 2.
- Show
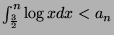 .
.
- 3.
- Setting
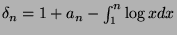 , show that,
when
, show that,
when
 ,
, 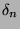 converges to a constant.
converges to a constant.
- 4.
- Denoting the converging value of
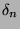 by
by 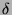 , show
exists, and compute its value.
, show
exists, and compute its value.
- 1.
-
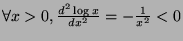 , that is
, that is
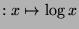 is concave.
We thus have the following inequality:
From which we deduce the sequence below:
is concave.
We thus have the following inequality:
From which we deduce the sequence below:
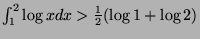
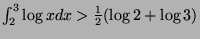
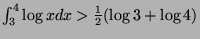
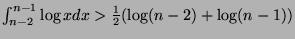
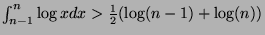
And therefore:
- 2.
-
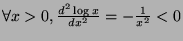 , that is
, that is
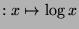 is concave.
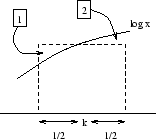
Thus, the area denoted 1 is larger than the one denoted 2 on the previous figure.
We thus have the following inequality:
From which we deduce the sequence below:
is concave.
Thus, the area denoted 1 is larger than the one denoted 2 on the previous figure.
We thus have the following inequality:
From which we deduce the sequence below:
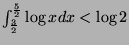
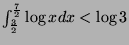
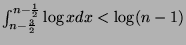
and
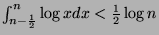
And therefore:
- 3.
-
Thus,
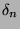 has upper and lower limits. Let us determine whether
has upper and lower limits. Let us determine whether 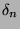 is increasing or decreasing:
is increasing or decreasing:
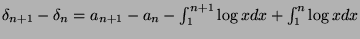
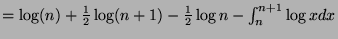
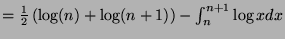
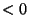 as we saw above.
as we saw above.
This means that 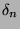 is decreasing with a lower limit, thus it converges to a constant we shall call
is decreasing with a lower limit, thus it converges to a constant we shall call
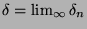 .
.
- 4.
-
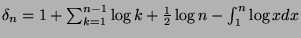
![$ = 1 + \log n! -\frac{1}{2}\log n - \left[ x(\log x - 1)\right]_1^n $](img1092.png)
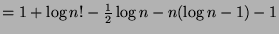
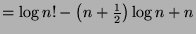
But,
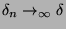 . Which means that:
. Which means that:
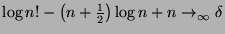
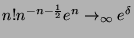
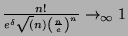



Next: Information Science I
Up: Mathematics
Previous: Problem 1 - Norms
Reynald AFFELDT
2000-06-08
![]() , define
, define ![]() by
by
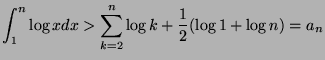
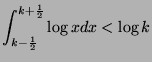
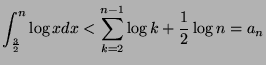
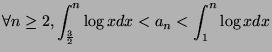
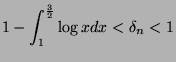
![]() is decreasing with a lower limit, thus it converges to a constant we shall call
is decreasing with a lower limit, thus it converges to a constant we shall call
![]() .
.